题目内容
【题目】已知函数
．
(1)试作出
的图象,并根据图象写出的单调区间；
(2)若函数
有两个零点,求实数b的取值范围．
【答案】(1)图象见解析，
的单调递减区间为（–∞，1）, 的单调递增区间为[1，+∞）；(2)（0，2）
【解析】
(1)利用绝对值的性质和指数函数的单调性把函数的解析式化成分段函数的形式,在直角坐标系内画出函数图象即可,通过函数的图象写出的单调区间；
(2)由题意可知：
有两个零点,即
有两个不同的实数解,可以转化为
有两个交点,利用图象可以求出
的取值范围.
(1) 
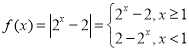,函数的图象如下图：
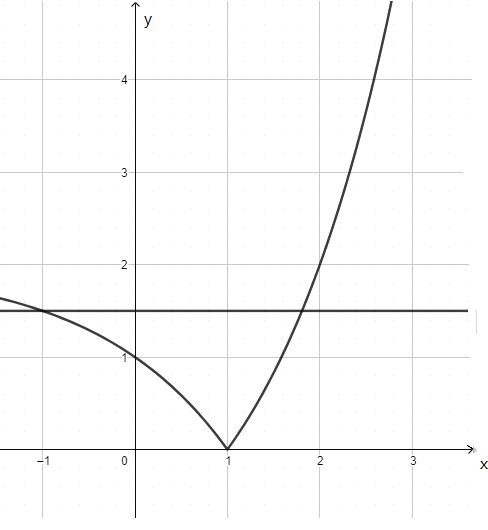
通过图象可知：的单调递减区间为（–∞，1）, 的单调递增区间为[1，+∞）；
(2)因为有两个零点,所以有两个不同的实数解,即有两个交点,如上图：通过图象可知：实数b的取值范围为（0，2）.
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
