题目内容
12.已知数列{an}中,a1=1,an+1=2nan(k∈N*).(1)求an;
(2)若bn=log2($\frac{{a}_{n}}{{4}^{n}}$),又数列{cn}的前n项和为bn,求数列{|cn|}的前n项和Sn.
分析 (1)运用恒等式an=a1•$\frac{{a}_{2}}{{a}_{1}}$•$\frac{{a}_{3}}{{a}_{2}}$…$\frac{{a}_{n}}{{a}_{n-1}}$,结合等差数列的求和公式,可得通项;
(2)求得bn=$\frac{{n}^{2}-5n}{2}$,运用通项和求和的关系,可得cn=n-3,再讨论当n≤3时,当n>3时,运用等差数列的求和公式,计算即可得到所求.
解答 解:(1)由题意可得an=a1•$\frac{{a}_{2}}{{a}_{1}}$•$\frac{{a}_{3}}{{a}_{2}}$•…•$\frac{{a}_{n}}{{a}_{n-1}}$
=1•2•4•…•2n-1=21+2+…+n-1=${2}^{\frac{n(n-1)}{2}}$,
可得an=${2}^{\frac{n(n-1)}{2}}$;
(2)bn=log2($\frac{{a}_{n}}{{4}^{n}}$)=log2${2}^{\frac{{n}^{2}-5n}{2}}$=$\frac{{n}^{2}-5n}{2}$,
当n=1时,c1=b1=-2;
当n>1时,cn=bn-bn-1=$\frac{{n}^{2}-5n}{2}$-$\frac{(n-1)^{2}-5(n-1)}{2}$
=n-3.对n=1也成立,
则cn=n-3,
当n≤3时,前n项和Sn=-bn=$\frac{5n-{n}^{2}}{2}$;
当n>3时,Sn=bn-2b3=$\frac{{n}^{2}-5n}{2}$+6=$\frac{{n}^{2}-5n+12}{2}$.
点评 本题考查等差数列的通项公式的运用,考查累乘法的运用和分类讨论的思想方法,属于中档题.

练习册系列答案
相关题目
17.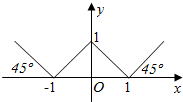 函效y=f(x)的图象如图所示,则y=f(x)的解析式是( )
函效y=f(x)的图象如图所示,则y=f(x)的解析式是( )
 函效y=f(x)的图象如图所示,则y=f(x)的解析式是( )
函效y=f(x)的图象如图所示,则y=f(x)的解析式是( )| A. | f(x)=$\left\{\begin{array}{l}{1-x,x<1}\\{x-1,x≥1}\end{array}\right.$ | |
| B. | f(x)=$\left\{\begin{array}{l}{-x-1,x<-1}\\{1+x,-1≤x<0}\\{1-x,0≤x≤1}\\{x-1,x>1}\end{array}\right.$ | |
| C. | f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,x>1或x<-1}\\{1-{x}^{2},-1≤x≤1}\end{array}\right.$ | |
| D. | f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x+1,x≤0}\\{{x}^{2}-2x+1,x>0}\end{array}\right.$ |
4.非零向量 $\overrightarrow{a}$,$\overrightarrow{b}$夹角为120°,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围为( )
| A. | [1,$\sqrt{3}$] | B. | [2,$\frac{4\sqrt{3}}{3}$] | C. | [$\frac{2\sqrt{3}}{3}$,4) | D. | [1,2] |