题目内容
(本小题满分12分)
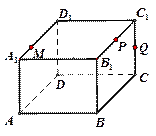
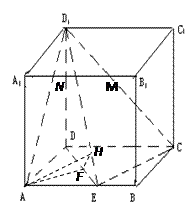
在长方体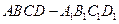 中,
中,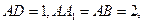 点
点 是
是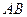 上的动点,点
上的动点,点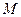 为
为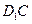 的中点.
的中点.
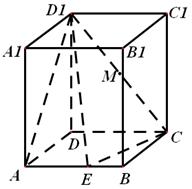
(1)当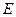 点在何处时,直线
点在何处时,直线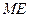 //平面
//平面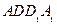 ,并证明你的结论;
,并证明你的结论;
(2)在(Ⅰ)成立的条件下,求二面角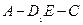 的大小.
的大小.
在长方体
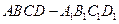 中,
中,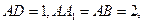 点
点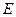 是
是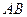 上的动点,点
上的动点,点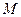 为
为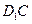 的中点.
的中点. 
(1)当
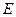 点在何处时,直线
点在何处时,直线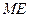 //平面
//平面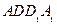 ,并证明你的结论;
,并证明你的结论;(2)在(Ⅰ)成立的条件下,求二面角
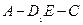 的大小.
的大小.证明:(Ⅰ)当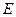 为
为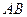 的中点时,
的中点时,
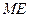 ∥平面
∥平面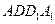 .
.
证明:取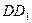 的中点N,连结MN、AN、
的中点N,连结MN、AN、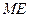 ,
,
 MN∥
MN∥ ,AE∥
,AE∥ ,
,
 四边形MNAE为平行四边形,可知 ME∥AN
四边形MNAE为平行四边形,可知 ME∥AN

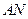 在平面
在平面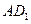 内
内
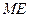 ∥平面
∥平面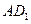 .
.
方法二)延长 交
交 延长线于
延长线于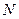 ,连结
,连结 .
.
 ∥
∥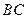
 ,又
,又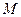 为
为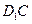 的中点,
的中点,
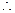
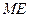 ∥
∥


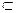 平面
平面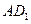
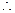
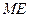 ∥平面
∥平面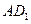 .
.
(Ⅱ)当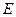 为
为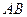 的中点时,
的中点时, ,
, 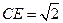 ,又
,又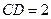 ,
,
可知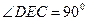 ,所以
,所以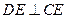 ,平面
,平面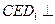 平面
平面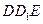 ,
,
所以二面角 的大小为
的大小为 ;高
;高
又二面角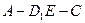 的大小为二面角
的大小为二面角 与二面角
与二面角 大小的和,
大小的和,
只需求二面角 的大小即可;
的大小即可;
过A点作 交DE于F,则
交DE于F,则 平面
平面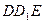 ,
,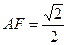 ,
,
过F作 于H,连结AH,
于H,连结AH,
则 AHF即为二面角
AHF即为二面角 的平面角,
的平面角,
 ,
, ,
, ,
,
所以二面角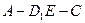 的大小为
的大小为 .
.
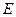 为
为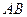 的中点时,
的中点时,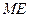 ∥平面
∥平面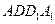 .
. 证明:取
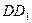 的中点N,连结MN、AN、
的中点N,连结MN、AN、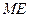 ,
, MN∥
MN∥ ,AE∥
,AE∥ ,
, 四边形MNAE为平行四边形,可知 ME∥AN
四边形MNAE为平行四边形,可知 ME∥AN
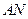 在平面
在平面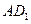 内
内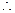
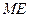 ∥平面
∥平面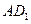 .
. 方法二)延长
 交
交 延长线于
延长线于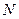 ,连结
,连结 .
. ∥
∥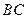
 ,又
,又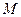 为
为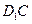 的中点,
的中点,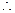
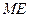 ∥
∥


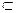 平面
平面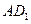
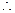
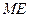 ∥平面
∥平面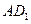 .
.(Ⅱ)当
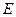 为
为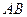 的中点时,
的中点时, ,
, 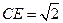 ,又
,又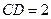 ,
,可知
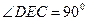 ,所以
,所以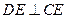 ,平面
,平面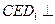 平面
平面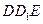 ,
,所以二面角
 的大小为
的大小为 ;高
;高又二面角
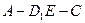 的大小为二面角
的大小为二面角 与二面角
与二面角 大小的和,
大小的和,只需求二面角
 的大小即可;
的大小即可;过A点作
 交DE于F,则
交DE于F,则 平面
平面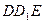 ,
,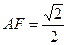 ,
,过F作
 于H,连结AH,
于H,连结AH,则
 AHF即为二面角
AHF即为二面角 的平面角,
的平面角,  ,
, ,
, ,
,所以二面角
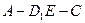 的大小为
的大小为 .
.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,四棱锥
,四棱锥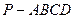 的底面是边长为
的底面是边长为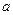 的菱形,
的菱形,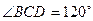 ,
,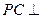 平面
平面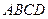 ,
,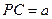 ,
,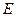 为
为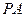 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;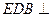 平面
平面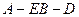 的正切值。
的正切值。
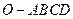 中,底面
中,底面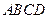 是边长为1的菱形,
是边长为1的菱形,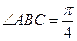 ,
, 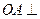 底面
底面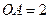 ,
,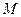 为
为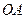 的中点.
的中点.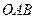 与平面
与平面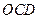 所成的二面角的余弦值.
所成的二面角的余弦值.
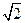 ,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点.
,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点.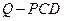 的体积为
的体积为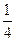 ?若存在,求出
?若存在,求出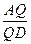 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。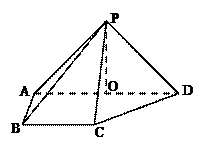
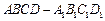 中,
中,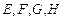 分别是棱
分别是棱 的中点.
的中点.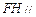 平面
平面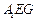 ;
;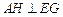 ;
;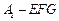 的体积.
的体积.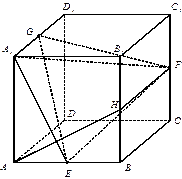
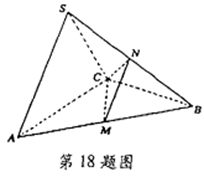
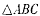 是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,
是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,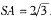 ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.
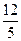 B
B
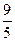 C.
C.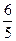 D.
D.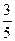
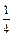 ,且
,且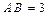 ,
,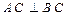 ,则球面的面积为 .
,则球面的面积为 .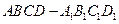 的棱长为4,P、Q分别为棱
的棱长为4,P、Q分别为棱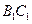 、
、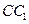 上的中点,M在
上的中点,M在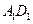 上,且
上,且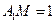 ,过P、Q、M的平面与
,过P、Q、M的平面与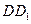 交于点N,则MN= .
交于点N,则MN= .