题目内容
已知函数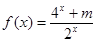 是奇函数.
是奇函数.
(1)求m的值:
(2)设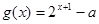 .若函数
.若函数 与
与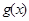 的图象至少有一个公共点.求实数a的取值范围.
的图象至少有一个公共点.求实数a的取值范围.
(1)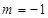 . (2)
. (2)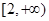 .
.
解析试题分析:((1)由函数 是奇函数可知:
是奇函数可知: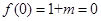 , 即得
, 即得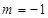 .
.
(2)根据函数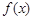 与
与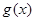 的图象至少有一个公共点,转化得到方程
的图象至少有一个公共点,转化得到方程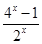
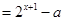 至少有一个实根.即方程
至少有一个实根.即方程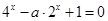 至少有一个实根 ,令
至少有一个实根 ,令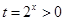 ,则方程
,则方程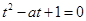 至少有一个正根.
至少有一个正根.
接下来可有两种思路,一是通过分离参数,应用基本不等式;二是利用二次函数知识.
试题解析:(1)由函数 是奇函数可知:
是奇函数可知: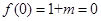 , 2分
, 2分
解得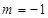 . 4分
. 4分
(2)函数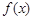 与
与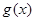 的图象至少有一个公共点
的图象至少有一个公共点
即方程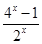
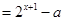 至少有一个实根 6分
至少有一个实根 6分
即方程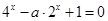 至少有一个实根 8分
至少有一个实根 8分
令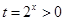 ,则方程
,则方程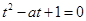 至少有一个正根
至少有一个正根
方法一:由于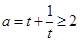
∴a的取值范围为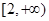 . 12分
. 12分
方法二:令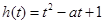 ,由于
,由于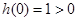 ,所以只须
,所以只须 ,
,
解得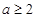 .
.
∴a的取值范围为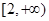 .
.
考点:函数的奇偶性,指数函数的性质,二次函数的性质,基本不等式.

练习册系列答案
相关题目
 的定义域为
的定义域为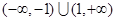 ,对定义域内的任意x,满足
,对定义域内的任意x,满足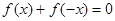 ,当
,当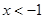 时,
时,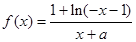 (a为常),且
(a为常),且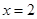 是函数
是函数 时,不等式
时,不等式 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;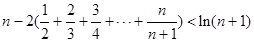
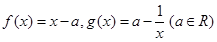 .
. 在
在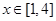 的单调性并用定义证明;
的单调性并用定义证明;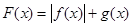 ,求
,求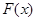 在区间
在区间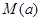 .
. 满足
满足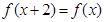 ,当
,当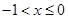 时
时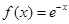 ;当
;当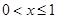 时
时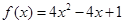 .
.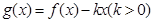 ,求函数
,求函数 在
在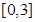 上的零点个数.
上的零点个数. .
. 有两个零点,求
有两个零点,求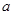 的取值范围;
的取值范围; 与
与 上各有一个零点,求
上各有一个零点,求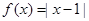
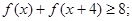
 .求证:
.求证: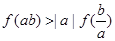 .
.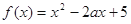 (
(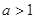 ).
). 的定义域和值域均是
的定义域和值域均是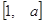 ,求实数
,求实数 的值;
的值;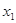 ,
,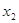
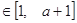 ,总有
,总有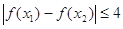 ,求实数
,求实数 的取值范围.
的取值范围. 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米
 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.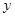 关于
关于