题目内容
已知函数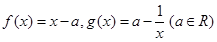 .
.
(1)判断函数 在
在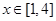 的单调性并用定义证明;
的单调性并用定义证明;
(2)令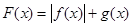 ,求
,求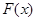 在区间
在区间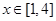 的最大值的表达式
的最大值的表达式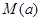 .
.
(1)函数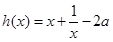 在
在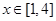 递增;证明详见答案解析.
递增;证明详见答案解析.
(2)当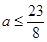 时,
时,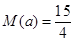 ;当
;当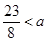 时,
时,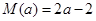 .
.
解析试题分析:(1)先根据已知条件求出 ,再根据单调性的定义证明即可;
,再根据单调性的定义证明即可;
(2)由(1)先求出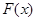 的表达式,再根据单调性求得各个区间的最大值,综上即可求出
的表达式,再根据单调性求得各个区间的最大值,综上即可求出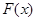 在区间
在区间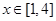 的最大值的表达式
的最大值的表达式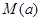 .
.
试题解析:(1)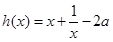 在
在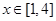 递增;
递增;
证明如下:
在区间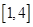 上任取
上任取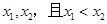
则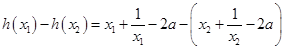

而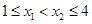 ,所以
,所以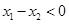 ,
,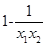 >0
>0
所以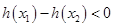 ,即函数
,即函数 在
在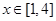 的单调递增;(6分)
的单调递增;(6分)
(2)若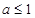 ,
,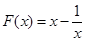 ,在
,在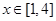 递增,
递增,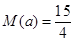 ,
,
若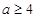 ,
,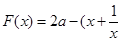 )在
)在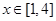 递减,
递减,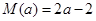 , (9分)
, (9分)
若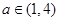 ,则
,则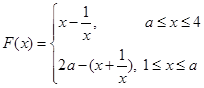 (11分)
(11分)
当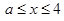 时,函数递增,
时,函数递增,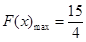 ,
,
当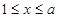 时,函数递减,
时,函数递减,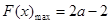 ; (13分)
; (13分)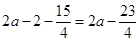 ,当
,当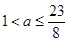 时,
时,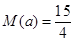 ,当
,当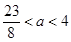 时,
时,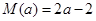 .
.
综上: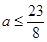 时,
时,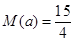 ,当
,当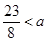 时,
时,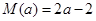 . (15分)
. (15分)
考点:函数的单调性、分段函数求值域问题.

练习册系列答案
相关题目
 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 米,圆心角为
米,圆心角为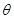 (弧度).
(弧度).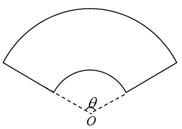
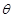 关于
关于 ,求
,求 的函数关系式,并求出
的函数关系式,并求出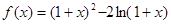
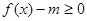 在
在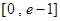 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;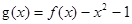 ,若关于x的方程
,若关于x的方程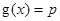 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.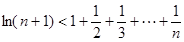
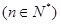
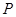 的关系允许近似的满足:
的关系允许近似的满足: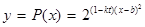 (其中
(其中 为关税的税率,且
为关税的税率,且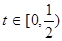 ,
, 为市场价格,
为市场价格,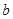 、
、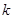 为正常数),当
为正常数),当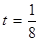 时的市场供应量曲线如图:
时的市场供应量曲线如图: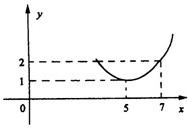
 ,它近似满足
,它近似满足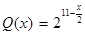 .当
.当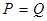 时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率
时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率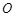 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点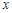 米,圆心角为
米,圆心角为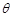 (弧度).
(弧度).
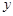 ,求
,求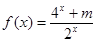 是奇函数.
是奇函数.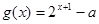 .若函数
.若函数 与
与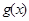 的图象至少有一个公共点.求实数a的取值范围.
的图象至少有一个公共点.求实数a的取值范围. 满足在集合
满足在集合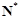 上的值域仍是集合
上的值域仍是集合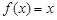 就是N函数.
就是N函数.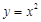 ,②
,②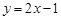 ,③
,③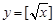 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果);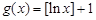 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;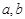 ,函数
,函数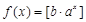 都不是N函数.
都不是N函数. ”表示不超过
”表示不超过 的最大整数)
的最大整数)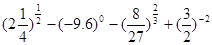 ;⑵
;⑵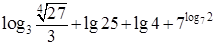 .
.