题目内容
已知函数 的定义域为
的定义域为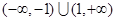 ,对定义域内的任意x,满足
,对定义域内的任意x,满足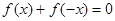 ,当
,当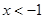 时,
时,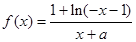 (a为常),且
(a为常),且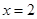 是函数
是函数 的一个极值点,
的一个极值点,
(1)求实数a的值;
(2)如果当 时,不等式
时,不等式 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(3)求证: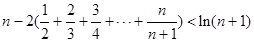
(1)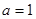 ;(2)2;(3)详见解析.
;(2)2;(3)详见解析.
解析试题分析:(1)利用 为奇函数,所以设
为奇函数,所以设 ,利用
,利用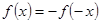 ,求出
,求出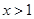 时的
时的 ,然后再求
,然后再求 时的
时的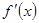 ,再根据
,再根据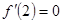 ,求出
,求出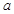 ,验证所求
,验证所求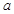 能够使
能够使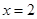 是函数
是函数 的一个极值点;(2)不等式
的一个极值点;(2)不等式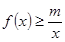 恒成立,转化为
恒成立,转化为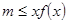 恒成立,设
恒成立,设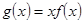 ,即求
,即求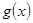 的最小值,求
的最小值,求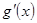
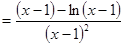 ,再设
,再设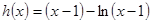 ,易求
,易求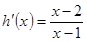 ,当
,当 时,
时,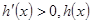 为增函数,
为增函数,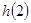 最小,
最小,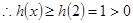 ,即
,即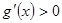 逐步分析
逐步分析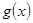 为单调递增函数,从而求得最小值.(3)通过
为单调递增函数,从而求得最小值.(3)通过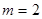 代入(2)式恒成立不等式
代入(2)式恒成立不等式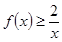 ,变形放缩后得到
,变形放缩后得到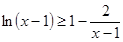 ,为出现(2)要证形式,所以令
,为出现(2)要证形式,所以令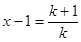 ,则
,则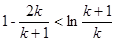 ,然后将k=1,2, n,代入上式,累加,从而得出要证不等式.此题综合性较强.
,然后将k=1,2, n,代入上式,累加,从而得出要证不等式.此题综合性较强.
试题解析:(1)由题知对定义域内任意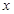 ,
,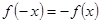 ,
,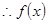 为奇函数,
为奇函数,
当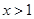 时,
时,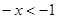 ,
, ,
,
当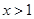 时,
时,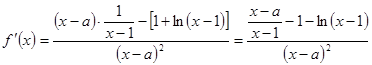
由题知: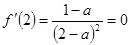 ,解得
,解得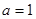 ,经验证,满足题意.
,经验证,满足题意.
(2)由(1)知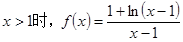
当 时,
时,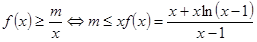 ,令
,令
则 时,
时,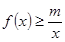 恒成立,转化为
恒成立,转化为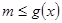 在
在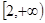 恒成立.
恒成立.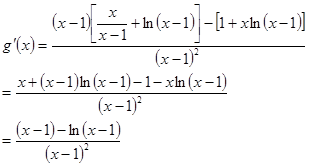
令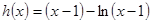 ,
,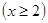 ,则
,则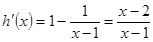 ,
,
当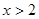 时,
时,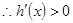 ,
,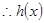 在
在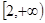 上单调递增.
上单调递增.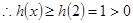
 当
当 时,
时,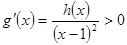 ,
,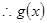 在
在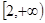 单调递增.
单调递增.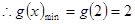
则若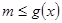 在
在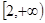 恒成立,则
恒成立,则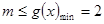
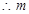 的最大值2.
的最大值2.
(3)由(2)知当 时,有
时,有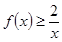 ,即
,即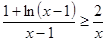
则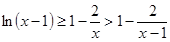
令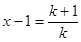 ,则
,则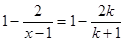

练习册系列答案
相关题目
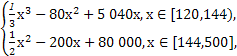
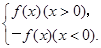 若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立. 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 米,圆心角为
米,圆心角为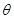 (弧度).
(弧度).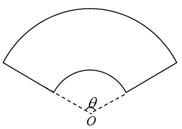
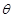 关于
关于 ,求
,求 的函数关系式,并求出
的函数关系式,并求出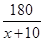 ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2=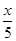 (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).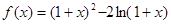
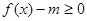 在
在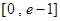 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;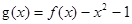 ,若关于x的方程
,若关于x的方程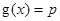 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.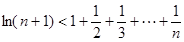
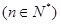
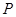 的关系允许近似的满足:
的关系允许近似的满足: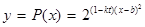 (其中
(其中 为关税的税率,且
为关税的税率,且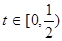 ,
, 为市场价格,
为市场价格,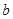 、
、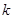 为正常数),当
为正常数),当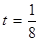 时的市场供应量曲线如图:
时的市场供应量曲线如图: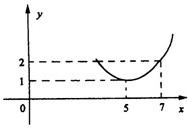
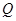 ,它近似满足
,它近似满足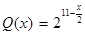 .当
.当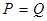 时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率
时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率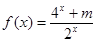 是奇函数.
是奇函数.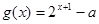 .若函数
.若函数 与
与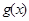 的图象至少有一个公共点.求实数a的取值范围.
的图象至少有一个公共点.求实数a的取值范围. ,两个函数
,两个函数 ,
, 的图像关于直线
的图像关于直线 对称.
对称. 满足的关系式;
满足的关系式; 取何值时,函数
取何值时,函数 有且只有一个零点;
有且只有一个零点; 时,在
时,在 上解不等式
上解不等式 .
.