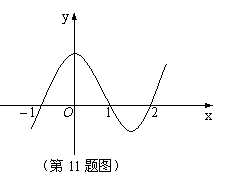
题目内容
在平面几何中,已知“正三角形内一点到三边距离之和是一个定值”,类比到空间写出你认为合适的结论: . .
正四面体(正方体)内一点到四(六)个面的距离之和是一个定值.
分析:根据平面中的某些性质类比推理出空间中的某些性质,一般遵循“点到线”,“线到面”,“面到体”等原则,由在平面几何中,已知“正三角形内一点到三边距离之和是一个定值”,是一个与线有关的性质,由此可以类比推出空间中一个与面有关的性质,由此即可得到答案.
解答:解:∵平面几何中,已知“正三角形内一点到三边距离之和是一个定值”,
根据平面中边的性质可类比为空间中面的性质
则我们可以将“正三角形”类比为“正四面体”(或“正六面体”,即“正方体”)
“到三边距离之和”类比为“到四(六)个面的距离之和”
故答案为:正四面体(正方体)内一点到四(六)个面的距离之和是一个定值
点评:本题考查的知识点是类比推理,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
相关题目
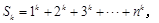 当
当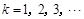 时,观察下列等式:
时,观察下列等式: ,
, ,
,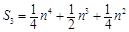 ,
, ,
,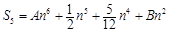 ,
,

 A大拇指
A大拇指 得出的一般性结论是 ( )
得出的一般性结论是 ( )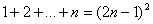 (
(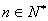 )
) (
( (
( (
( ,
, ,
, 根据上述规律,
根据上述规律, ( )
( )



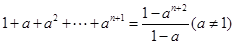 ”,在验证
”,在验证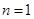 成立时,等号左边的式子是
成立时,等号左边的式子是 .
. ,它的内切
,它的内切 圆半径为
圆半径为 ,则
,则 ,由此类比得:已知正四面体的高为H,它的内切球半径为
,由此类比得:已知正四面体的高为H,它的内切球半径为 ,则
,则 .
.