题目内容
9.在△ABC中,∠B=30°,∠A=90°,M是边BC的中点,现将△ABM沿AM旋转,当△ABM转到与△ACM所在面垂直时,CB与平面AMC所成的角的正弦值为$\frac{\sqrt{30}}{10}$;异面直线CB与AM所成角的余弦值是$\frac{\sqrt{10}}{5}$.
分析 (1)利用好折叠前后图形的关系,作BE垂直AMd 延长线与E点,连接EC,作OC⊥AM
计算线段长度,转化为三角Rt△BEC中求解.
(2)建立空间坐标系转化为向量$\overrightarrow{BC}$与$\overrightarrow{AM}$夹角求解,利用向量的数量积.
解答 解:(1)∵在△ABC中,∠B=30°,∠A=90°,M是边BC的中点,
∴作BE垂直AM延长线与E点,连接EC,作OC⊥AM,
设AC=1,则AB=$\sqrt{3}$,MA=MB=MC=1,
根据平面几何知识得出;BE=$\frac{\sqrt{3}}{2}$,ME=$\frac{1}{2}$,
EC=$\sqrt{1+\frac{1}{4}-2×1×\frac{1}{2}×(-\frac{1}{2})}$=$\frac{\sqrt{7}}{2}$,
OC=$\frac{\sqrt{3}}{2}$,OA=OM=$\frac{1}{2}$,
∵将△ABM沿AM旋转,当△ABM转到与△ACM所在面垂直,
∴BE⊥面AEC,
CB与平面AMC所成的角θ=∠BCE,
∴Rt△BEC中,BC=$\frac{\sqrt{10}}{2}$,OE=1,
sinθ=$\frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{10}}{2}}$=$\frac{\sqrt{30}}{10}$;
(2)建立空间坐标系如图所示,
∴B(0,0,$\frac{\sqrt{3}}{2}$),E(0,0,0),C($\frac{\sqrt{3}}{2}$,1,0),
$\overrightarrow{BC}$=($\frac{\sqrt{3}}{2}$,1,-$\frac{\sqrt{3}}{2}$),$\overrightarrow{AM}$=(0,1,0)
∵$\overrightarrow{BC}$$•\overrightarrow{AM}$=1,|$\overrightarrow{BC}$|=$\sqrt{\frac{3}{4}+\frac{3}{4}+1}$=$\frac{\sqrt{10}}{2}$,|$\overrightarrow{AM}$|=1,
∴cos<$\overrightarrow{BC}$,$\overrightarrow{AM}$>=$\frac{1}{\frac{\sqrt{10}}{2}×1}$=$\frac{\sqrt{10}}{5}$,
∴异面直线CB与AM所成角的余弦值是$\frac{\sqrt{10}}{5}$
故答案为:$\frac{\sqrt{30}}{10}$;$\frac{\sqrt{10}}{5}$.
点评 本题考查了折叠问题,求解夹角,充分利好平面图形与立体图形的关系,考查了学生的运算能力,思维能力.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |

 如图,在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是BB1,BC的中点,(1)直线MN与平面BDD1B1所成角的余弦值为$\frac{\sqrt{3}}{2}$
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是BB1,BC的中点,(1)直线MN与平面BDD1B1所成角的余弦值为$\frac{\sqrt{3}}{2}$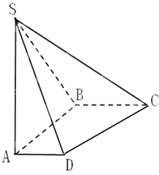 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$