题目内容
【题目】已知函数![]() .
.
(Ⅰ)求证:1是函数![]() 的极值点;
的极值点;
(Ⅱ)设![]() 是函数
是函数![]() 的导函数,求证:
的导函数,求证: ![]() .
.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析.
【解析】试题分析:(Ⅰ)求函数的导数,分析导数在1两侧的符号,判定1是极值点;(Ⅱ)求出![]() 的导数,找到
的导数,找到![]() ,列表求出函数的最小值即可证明.
,列表求出函数的最小值即可证明.
试题解析:(Ⅰ)证明:
证法1: ![]() 的定义域为
的定义域为![]()
由![]() 得
得
![]() ,
, ![]() .
.
当![]() 时,
时, ![]() ,
, ![]() ,故
,故![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,
, ![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减;
所以1是函数![]() 的极值点.
的极值点.
证法2:(根据极值的定义直接证明)
![]() 的定义域为
的定义域为![]()
![]() ,
, ![]()
当![]() 时,
时, ![]() ,即
,即![]() ;
;
当![]() 时,
时, ![]() ,即
,即![]() ;
;
根据极值的定义,1是![]() 的极值点.
的极值点.
(Ⅱ)由题意可知, ![]()
证法1: ![]() ,
,
令![]() ,
,
![]() ,故
,故![]() 在
在![]() 上单调递增. 又
上单调递增. 又![]() ,又
,又![]() 在
在![]() 上连续,
上连续,
![]() 使得
使得![]() ,即
,即![]() ,
,
![]()
![]() .(*)
.(*)
![]() 随x的变化情况如下:
随x的变化情况如下:
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
………………10分
![]()
![]() .
.
由(*)式得![]() ,代入上式得
,代入上式得
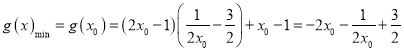 .
.
令![]() ,
,
![]() ,故
,故![]() 在
在![]() 上单调递减.
上单调递减.
![]() ,又
,又![]() ,
, ![]() .
.
即![]()
![]() .
.
证法2: ![]() ,
,
令![]() ,
,
![]() 随x的变化情况如下:
随x的变化情况如下:
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时取到等号.
时取到等号.
![]() ,令
,令![]() 得
得![]() .
.
![]() 随x的变化情况如下:
随x的变化情况如下:
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时取到等号.
时取到等号. ![]() .即
.即![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.
