题目内容
【题目】已知f(x)为定义在R上的奇函数,当x≥0,f(x)=log3(x+3)﹣a,则不等式|f(x)|<1的解集为 .
【答案】(﹣6,6)
【解析】解:f(x)为定义在R上的奇函数, 当x≥0,f(x)=log3(x+3)﹣a,
∴f(0)=log33﹣a=0,
解得a=1;
∴x≥0时,f(x)=log3(x+3)﹣1,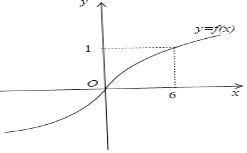
令f(x)=1,即log3(x+3)﹣1=1,
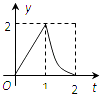
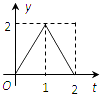
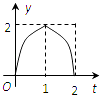
解得x=6,根据奇函数的性质画出函数图象,如图所示;
结合函数f(x)的图象,得出不等式|f(x)|<1的解集为(﹣6,6).
所以答案是:(﹣6,6).
【考点精析】解答此题的关键在于理解指、对数不等式的解法的相关知识,掌握指数不等式的解法规律:根据指数函数的性质转化;对数不等式的解法规律:根据对数函数的性质转化.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了调查喜爱运动是否和性别有关,我们随机抽取了50名对象进行了问卷调查得到了如下的2×2列联表:
喜爱运动 | 不喜爱运动 | 合计 | |
男性 | 5 | ||
女性 | 10 | ||
合计 | 50 |
若在全部50人中随机抽取2人,抽到喜爱运动和不喜爱运动的男性各一人的概率为 ![]() .
.
附:
P(K2≥k) | 0.05 | 0.01 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2= ![]()
(1)请将上面的2×2列联表补充完整;
(2)能否在犯错误的概率不超过0.001的前提下认为喜爱运动与性别有关?说明你的理由..
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下![]() 的列联表:
的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式 ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确的是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错语的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C. 有99%以上的把握认为“爱好该项运动与性别无关”
D. 有99%以上的把握认为“爱好该项运动与性别有关”