题目内容
【题目】(本小题满分12分)
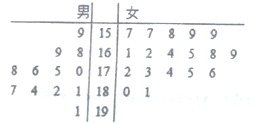
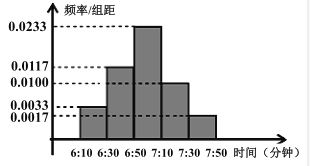
某学校简单随机抽样方法抽取了100名同学,对其日均课外阅读时间:(单位:分钟)进行调查,结果如下:

若将日均课外阅读时间不低于60分钟的学生称为“读书迷”
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
①求抽取的4为同学中有男同学又有女同学的概率;
②记抽取的“读书迷”中男生人数为X,求X的分布列和数学期望.
【答案】(1)320 (2)![]() ,
, ![]()
【解析】试题分析:抽取的100名同学读书时间不低于60分钟的有8人,占![]() ,估计出4000名同学中“读书迷”的人数,8名同学中有3名男生5名女生,抽取4名有男生又有女生的对立事件是只抽取4名女生,利用对立事件概率公式求出,
,估计出4000名同学中“读书迷”的人数,8名同学中有3名男生5名女生,抽取4名有男生又有女生的对立事件是只抽取4名女生,利用对立事件概率公式求出, ![]() 表示抽取的男生人数可取值为0,1,2,3,分四种情况求出对应的概率值及数学期望.
表示抽取的男生人数可取值为0,1,2,3,分四种情况求出对应的概率值及数学期望.
试题解析:
(Ⅰ)设该校4000名学生中“读书迷”有x人,则![]() =
=![]() ,解得x=320.
,解得x=320.
所以该校4000名学生中“读书迷”有320人.
(Ⅱ)(ⅰ)抽取的4名同学既有男同学,又有女同学的概率
P=![]() =
=![]() .
.
(ⅱ)X可取0,1,2,3.
P(X=0)=![]() =
=![]() , P(X=1)=
, P(X=1)=![]() =
=![]() ,
,
P(X=2)=![]() =
=![]() , P(X=3)=
, P(X=3)=![]() =
=![]() ,
,
X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E(X)=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】(本小题满分12分)
某学校用简单随机抽样方法抽取了100名同学,对其日均课外阅读时间(单位:分钟)进行调查,结果如下:
t |
|
|
|
|
|
|
男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
(i)求抽取的4位同学中既有男同学又有女同学的概率;
(ii)记抽取的“读书迷”中男生人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望