Question

【题目】已知圆C经过原点O，与x轴另一交点的横坐标为4，与y轴另一交点的纵坐标为2，
（1）求圆C的方程；
（2）已知点B的坐标为（0，2），设P，Q分别是直线l：x+y+2=0和圆C上的动点，求|PB|+|PQ|的最小值及此时点P的坐标．

Answer 1

【答案】
（1）解：∵圆C经过原点O，与x轴另一交点的横坐标为4，与y轴另一交点的纵坐标为2，

即点A（4，0），B（0，2）是圆的一条直径，

则圆心坐标为（2，1）．半径r= ，

则圆的方程为（x﹣2）2+（y﹣1）2=5．

（2）解：点B关于直线l：x+y+2=0的对称点为B′（﹣4，﹣2），

则|PB|+|PQ|=|PB′|+|PQ|≥|B′Q|，

又B′到圆上的点的最短距离为|B′C|﹣r，

∴|PB|+|PQ|的最小值为2 ，

直线B′C的方程为y= ，

则直线B′C与直线x+y+2=0的交点P的坐标满足 ，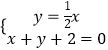

解得 ，即P（﹣ ，﹣ ）．

【解析】（1）结合条件即可求圆C的方程；（2）求出点B关于直线l：x+y+2=0的对称点，根据对称性的性质即可得到结论．