题目内容
【题目】已知椭圆C:![]() (a>b>0)的上、下、左、右四个顶点分别为A,B,C,D,x轴正半轴上的点P满足|PA|=|PD|=2,|PC|=4。
(a>b>0)的上、下、左、右四个顶点分别为A,B,C,D,x轴正半轴上的点P满足|PA|=|PD|=2,|PC|=4。
(I)求椭圆C的标准方程以及点P的坐标;
(II)过点P作直线l交椭圆C于点M,N,是否存在这样的直线l使得△MNA和△MND的面积相等?若存在,请求出直线l的方程,若不存在,请说明理由;
(III)在(II)的条件下,求当直线l的倾斜角为钝角时△MND的面积。
【答案】(1)![]() ,P点坐标为(1,0).(2)y=
,P点坐标为(1,0).(2)y=![]() (x-1)或y=
(x-1)或y=![]() (x-1).(3)
(x-1).(3)![]()
【解析】
试题(1)设点P的坐标,表示条件,解方程组可得a=3,x0=1,b=![]() .(2)先将条件转化为点A,D到直线l的距离相等. 再根据点到直线距离公式解直线斜率,即得直线l的方程,(3)将直线方程代人椭圆方程,利用韦达定理以及弦长公式求底边边长,再根据点到直线距离公式求高,最后代人面积公式求面积.
.(2)先将条件转化为点A,D到直线l的距离相等. 再根据点到直线距离公式解直线斜率,即得直线l的方程,(3)将直线方程代人椭圆方程,利用韦达定理以及弦长公式求底边边长,再根据点到直线距离公式求高,最后代人面积公式求面积.
试题解析:解:(I)设点P的坐标为(x0,0)(x0>0),易知2a=2+4,a=3,
x0=4-a=1,b=![]() .
.
因此椭圆标准方程为![]() ,P点坐标为(1,0).
,P点坐标为(1,0).
(II)设直线l:y=k(x-1).
由△MNA与△MND的面积相等,则点A,D到直线l的距离相等.
所以![]() ,解得k=
,解得k=![]() 或k=
或k=![]() .
.
所以直线l的方程为y=![]() (x-1)或y=
(x-1)或y=![]() (x-1).
(x-1).
(Ⅲ)若直线l倾斜角为钝角,即k=![]() ,此时方程为y=
,此时方程为y=![]() (x-1).
(x-1).
与椭圆方程![]() 联立
联立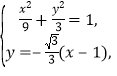 消x得
消x得![]() 。
。
设M,N坐标分别为(x1,y1),(x2,y2),
则有y1+y2=![]() ,y1y2=
,y1y2=![]() .
.
所以△MND的面积
S=![]() |PD|·|y1-y2|=
|PD|·|y1-y2|=![]() ×2×
×2×![]() =
=![]() 。
。
故所求△MND的面积为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目