题目内容
【题目】已知函数f(x)=4x+a2x+3,a∈R.
(1)当a=﹣4时,且x∈[0,2],求函数f(x)的值域;
(2)若关于x的方程f(x)=0在(0,+∞)上有两个不同实根,求实数a的取值范围.
【答案】
(1)解:当a=﹣4时,令t=2x,
由x∈[0,2],得t∈[1,4],y=t2﹣4t+3=(t﹣2)2﹣1
当t=2时,ymin=﹣1;当t=4时,ymax=3.
∴函数f(x)的值域为[﹣1,3]
(2)解:令t=2x,由x>0知t>1,且函数t=2x在(0,+∞)单调递增.
∴原问题转化为方程t2+at+3=0在(1,+∞)上有两个不等实根,求a的取值范围.
设g(t)=t2+at+3,则 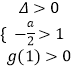 ,即
,即 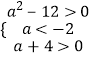 ,解得
,解得 ![]() .
.
∴实数a的取值范围是 ![]()
【解析】(1)把a=﹣4代入函数解析式,换元后利用配方法求函数f(x)的值域;(2)令t=2x , 由x的范围得到t的范围,则问题转化为方程t2+at+3=0在(1,+∞)上有两个不等实根,求a的取值范围.然后结合该二次方程对应的二次函数图象与t轴的交点列不等式组求解a的取值范围.
【考点精析】解答此题的关键在于理解二次函数在闭区间上的最值的相关知识,掌握当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() ,以及对函数的零点与方程根的关系的理解,了解二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.
,以及对函数的零点与方程根的关系的理解,了解二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目