题目内容
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左焦点
)的左焦点![]() 与抛物线
与抛物线![]() 的焦点重合,直线
的焦点重合,直线![]() 与以原点
与以原点![]() 为圆心,以椭圆的离心率
为圆心,以椭圆的离心率![]() 为半径的圆相切.
为半径的圆相切.
(Ⅰ)求该椭圆![]() 的方程;
的方程;
(Ⅱ)设点![]() 坐标为
坐标为![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)直线
;(Ⅱ)直线![]() 的方程为
的方程为![]() 或
或![]() .
.
【解析】试题分析:(I)由抛物线的方程,求得焦点坐标,即可求得c,利用点到直线的距离公式,求得椭圆的离心率,求得a和b的值,求得椭圆方程;
(II)分类讨论,当直线斜率存在时,代入椭圆方程,利用韦达定理及中点坐标公式,即可求得k的值,求得直线AB的方程.
试题解析:
(Ⅰ)依题意,得![]() ,
, 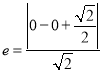
![]() ,即
,即![]() ,∴
,∴![]() ,
, ![]() ,
,
∴所求椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)若直线![]() 斜率不存在,即
斜率不存在,即![]() :
: ![]() ,满足
,满足![]() .
.
若直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,
,
将其代入![]() ,整理得
,整理得![]() ,
, ![]() ,
,
设![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
,
∴![]() 中点
中点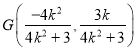 ,根据题意
,根据题意![]() ,
,
∴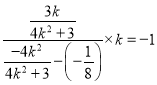 ,解得
,解得![]() ,
,
综上,直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目