题目内容
6.已知集合A={x|-x2+3x+10≥0},B={x|k+1≤x≤2k-1}.(Ⅰ)当A∩B=B时,求k的取值范围.
(Ⅱ)当A∩B=∅时,求实数k的取值范围.
分析 (Ⅰ)把集合A、B化简,借助于子集概念得到两集合端点值的关系,求解不等式得到k的范围
(Ⅱ)在(Ⅰ)化简后的基础上,由两集合的交集是空集得到两集合端点值的关系,从而求出k的范围;
解答 解:(Ⅰ)A={x|-x2+3x+10≥0}={x|-2≤x≤5],B={x|k+1≤x≤2k-1}.
∵A∩B=B,
∴B⊆A,
当B=∅,即k+1>2k-1,解得k<2,
当B≠∅,则$\left\{\begin{array}{l}{k+1≥-2}\\{2k-1≤5}\\{k+1≤2k-1}\end{array}\right.$或k+1>2k-1,解得2≤k≤3,
综上所述k的范围为(-∞.3];
(Ⅱ)当A∩B=∅时,
当B=∅,即k+1>2k-1,解得k<2,
当B≠∅,$\left\{\begin{array}{l}{k+1≤2k-1}\\{k+1>5}\end{array}\right.$或$\left\{\begin{array}{l}{2k-1<-2}\\{k+1≤2k-1}\end{array}\right.$,
解得k>4,
综上所述k的取值范围为(-∞,2)∪(4,+∞)
点评 本题考查了交集及其运算,考查了不等式的解法以及分类讨论思想,是中档题.

练习册系列答案
相关题目
14.已知函数y=f(x)在区间(0,2)上为增函数,函数y=f(x+2)为偶函数,则f(1),f($\frac{5}{2}$),f($\frac{7}{2}$)的大小关系是( )
| A. | f($\frac{5}{2}$)>f(1)>f($\frac{7}{2}$) | B. | f(1)>f($\frac{5}{2}$)>f($\frac{7}{2}$) | C. | f($\frac{7}{2}$)>f($\frac{5}{2}$)>f(1) | D. | f($\frac{7}{2}$)>f(1)>f($\frac{5}{2}$) |
15.下列说法中,一定成立的是( )
| A. | 若a>b,c>d,则ab>cd | B. | 若|a|<b,则a+b>0 | ||
| C. | 若a>b>0,则ab>ba | D. | 若$\frac{1}{a}>\frac{1}{b}$,则a<b |
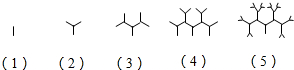 如图所示是按照一定规律画出的一列“树型”图,设第n个图有an个“树枝”,则an+1与an(n≥1)之间的关系是an+1=2an+1(n≥1).
如图所示是按照一定规律画出的一列“树型”图,设第n个图有an个“树枝”,则an+1与an(n≥1)之间的关系是an+1=2an+1(n≥1).