题目内容
17．
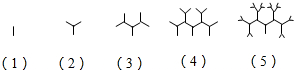如图所示是按照一定规律画出的一列“树型”图，设第n个图有an个“树枝”，则an+1与an（n≥1）之间的关系是an+1=2an+1（n≥1）．
分析 由已知中按照一定规律画出的一列“树型”图，分析第n个图中“树枝”an的变化规律，可得答案．
解答 解：由已知中按照一定规律画出的一列“树型”图，
可得第n个图中“树枝”an的变化规律：
a1=1，a2=3，a3=7，a4=15，a5=31，…
归纳可得：an=2n-1，
故an+1=2n+1-1，
故an+1=2an+1，
故答案为：an+1=2an+1（n≥1）
点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5．要从已编号（1到50）的50名学生中随机抽取5名学生参加问卷调查，用系统抽样方法确定所选取的5名学生的编号可能是（ ）
| A． | 5，10，15，20，25 | B． | 3，13，23，33，43 | C． | 1，2，3，4，5 | D． | 2，4，8，16，32 |
12．下面是一商场某一个时间制定销售计划的局部结构图，则“计划”受影响的主要因（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 7个 |
9．2015年田径世锦赛将于8月至9月在北京进行，为了搞好接待工作，组委会招募了16名男志愿者和14名女志愿者，调查发现，男、女志愿者中分别有12人和6人喜爱运动，其余不喜爱．
（1）根据2×2列联表数据，完成下列表格
（2）根据列联表的独立性检验，能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关？
（3）若用分层抽样方法从喜爱运动的志愿者中选6人，现须从抽取的6人中派2人去参加某项公益活动，问派去2人中恰有一名男生的概率．
（1）根据2×2列联表数据，完成下列表格
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 12 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
（3）若用分层抽样方法从喜爱运动的志愿者中选6人，现须从抽取的6人中派2人去参加某项公益活动，问派去2人中恰有一名男生的概率．