题目内容
设奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时t的取值范围是( ).
| A.-2≤t≤2 | B.- ≤t≤ ≤t≤ |
| C.t≤-2或t=0或t≥2 | D.t≤- 或t=0或t≥ 或t=0或t≥ |
C
解析

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
若函数
 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
方程 的解所在的区间是( )
的解所在的区间是( )
A. | B. | C. | D. |
已知函数f(x)的图像如图所示,则f(x)的解析式可以是( )
A.f(x)=x- | B.f(x)= | C.f(x)= -1 -1 | D.f(x)= |
已知f(x)是定义在(0,+∞) 上的非负可导函数,且满足xf′(x)+f(x)≤0,对任意的0<a<b,则必有( ).
| A.af(b)≤bf(a) | B.bf(a)≤af(b) |
| C.af(a)≤f(b) | D.bf(b)≤f(a) |
函数f(x)=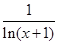 +
+ 的定义域为( ).
的定义域为( ).
| A.[-2,0)∪(0,2] | B.(-1,0)∪(0,2] |
| C.[-2,2] | D.(-1,2] |
函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)= ( ).
| A.ex+1 | B.ex-1 | C.e-x+1 | D.e-x-1 |
已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)= ,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围是( ).
,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围是( ).
A.0<k≤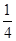 或k= 或k= | B.0<k≤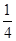 |
C.0<k<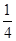 或k= 或k= | D.0<k<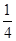 |
 的导函数
的导函数 的图象如图所示,那么函数
的图象如图所示,那么函数