题目内容
方程 的解所在的区间是( )
的解所在的区间是( )
A. | B. | C. | D. |
C
解析试题分析:设 ,则由指数函数与一次函数的性质可知,函数
,则由指数函数与一次函数的性质可知,函数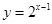 与
与 的
的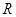 上都是递增函数,所以
上都是递增函数,所以 在
在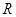 上单调递增,故函数
上单调递增,故函数 最多有一个零点,而
最多有一个零点,而 ,
, ,根据零点存在定理可知,
,根据零点存在定理可知, 有一个零点,且该零点处在区间
有一个零点,且该零点处在区间 内,故选答案C.
内,故选答案C.
考点:函数与方程.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
定义: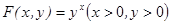 ,已知数列
,已知数列 满足:
满足:
 ,若对任意正整数
,若对任意正整数 ,都有
,都有
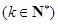 成立,则
成立,则 的值为( )
的值为( )
A. | B. | C.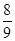 | D. |
函数 是( )
是( )
A.最小正周期为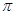 的偶函数 的偶函数 |
B.最小正周期为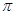 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的奇函数 的奇函数 |
已知函数 ,其中
,其中 为实数,若
为实数,若 对
对 恒成立,且
恒成立,且 ,则
,则 的单调递增区间是
的单调递增区间是
A. | B. |
C. | D. |
下列函数中既是奇函数又是 上的增函数的是( )
上的增函数的是( )
A.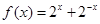 | B.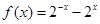 | C. | D. |
给出下列函数:
① ;②
;② ;③
;③ ;④
;④ .
.
则它们共同具有的性质是( )
| A.周期性 | B.偶函数 | C.奇函数 | D.无最大值 |
下列函数中,既是偶函数,又是在区间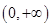 上单调递减的函数是( )
上单调递减的函数是( )
A. | B.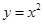 | C. | D. |
设奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时t的取值范围是( ).
| A.-2≤t≤2 | B.- ≤t≤ ≤t≤ |
| C.t≤-2或t=0或t≥2 | D.t≤- 或t=0或t≥ 或t=0或t≥ |
已知 ,
, ,则函数
,则函数 的图象必定不经过( )
的图象必定不经过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |