题目内容
设数列{an}满足:a1=1,an=a1+
a2+
a3+…+
an-1(n≥2,n∈N),若an=2009,则n= .
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:由题意,an+1-an=
,可得
=
,利用叠乘法,即可得出结论.
| an |
| n |
| an+1 |
| an |
| n+1 |
| n |
解答:
解:由题意,an+1-an=
,
∴
=
,
∴an=1×
×
×…×
=n,
∵an=2009,∴n=2009
故答案为:2009.
| an |
| n |
∴
| an+1 |
| an |
| n+1 |
| n |
∴an=1×
| 2 |
| 1 |
| 3 |
| 2 |
| n |
| n-1 |
∵an=2009,∴n=2009
故答案为:2009.
点评:本题考查数列递推式,考查学生的计算能力,确定
=
,利用叠乘法是关键.
| an+1 |
| an |
| n+1 |
| n |

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知f(x)=ax2+bx+c,且b>0,若对任意x有f(x)≥0,则
的最小值为( )
| f(1) |
| b |
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
已知F1(-c,0),F2(c,0)是双曲线C:
-
=1(a>0,b>0)的左右焦点,若p为双曲线右支上一点,满足
•
=4ac,∠F1PF2=
,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| π |
| 3 |
A、2
| ||||
B、
| ||||
| C、2 | ||||
D、
|
定义:F(x,y)=yx(x>0,y>0),已知数列{an}满足an=
(n∈N*),若对任意正整数n,都有an≥ak(k∈N*)成立,则ak的值为( )
| F(n,2) |
| F(2,n) |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
如果(3x+2)5=a0x5+a1x4+a2x3+a3x2+a4x+a5,那么a0-a1+a2-a3+a4的值等于( )
| A、33 | ||
| B、-31 | ||
C、
| ||
D、
|
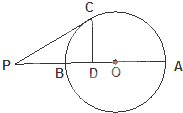 如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=
如图:AB是⊙O的直径,点P在AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=