题目内容
椭圆
（θ为参数）的离心率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：椭圆的参数方程
专题：圆锥曲线的定义、性质与方程,坐标系和参数方程
分析：根据参数方程和平方关系求出椭圆的标准方程，求出a、b、c，再求出椭圆的离心率e．
解答：
解：由
得，椭圆的标准方程为
+
=1，
所以a=5、b=4，则c=3，
所以椭圆的离心率e=
=
，
故选：C．
|
| x2 |
| 25 |
| y2 |
| 16 |
所以a=5、b=4，则c=3，
所以椭圆的离心率e=
| c |
| a |
| 3 |
| 5 |
故选：C．
点评：本题考查利用平方关系将椭圆的参数方程化为标准方程，以及椭圆的性质，属于基础题．
练习册系列答案
相关题目
设f（x）=xlnx，若f′（x0）=2，则x0等于（ ）
| A、e2 | ||
| B、e | ||
C、
| ||
| D、ln2 |
已知f（x）=ax2+bx+c，且b＞0，若对任意x有f（x）≥0，则
的最小值为（ ）
| f(1) |
| b |
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
已知数列{an}满足：a1=-
，an+1=1-
，则a2009=（ ）
| 1 |
| 4 |
| 1 |
| an |
A、
| ||
| B、5 | ||
C、-
| ||
D、
|
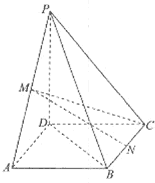如图，在四棱锥P-ABCD中，底面ABCD是正方形，PD⊥底面ABCD，M、N分别为PA、BC的中点，且PD=AD=1，