题目内容
【题目】设
是二次函数，方程
有两个相等的实根，且
（1）求
的表达式；
（2）求的图像与两坐标轴所围成图形的面积
【答案】（1）
；（2）
．
【解析】
试题（1）二次函数解析式的求法：根据已知条件确定二次函数的解析式，一般用待定系数法，选择规律如下：①已知三个点坐标，宜选用一般式；②已知顶点坐标、对称轴、最大（小）值，宜选用顶点式；③已知图象与
轴两交点的坐标，宜选用两根式；（2）用微积分基本定理求定积分，关键是求出被积函数的原函数，此外如果被积函数是绝对值函数或分段函数，那么可以利用定积分对积分区间的可加性，将积分区间分解，代入相应的解析式，分别求出积分值相加．
试题解析：（1）由
是二次函数且
，则可设
方程
由两个相等的实根，
，得到
（2）由可知它的图像与轴交于
，与
轴交于
记图像与两坐标轴所围成图形的面积为
，则
的图像与两坐标轴所围成图形的面积为．
天天向上一本好卷系列答案
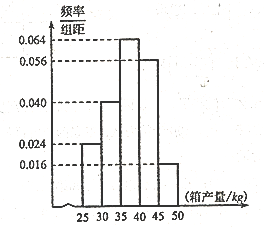
小学生10分钟应用题系列答案【题目】为积极响应国家“阳光体育运动”的号召，某学校在了解到学生的实际运动情况后，发起以“走出教室，走到操场，走到阳光”为口号的课外活动倡议。为调查该校学生每周平均体育运动时间的情况，从高一高二基础年级与高三三个年级学生中按照4:3:3的比例分层抽样，收集300位学生每周平均体育运动时间的样本数据(单位：小时)，得到如图所示的频率分布直方图。
（1）据图估计该校学生每周平均体育运动时间．并估计高一年级每周平均体育运动时间不足4小时的人数；
（2）规定每周平均体育运动时间不少于6小时记为“优秀”，否则为“非优秀”，在样本数据中，有30位高三学生的每周平均体育运动时间不少于6小时，请完成下列
列联表，并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”．
基础年级 | 高三 | 合计 | |
优秀 | |||
非优秀 | |||
合计 | 300 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附：K2
，n＝a+b+c+d．
【题目】某高校在2019的自主招生考试中，考生笔试成绩分布在
，随机抽取200名考生成绩作为样本研究，按照笔试成绩分成5组，得到的如下的频率分布表：
组号 | 分数区间 | 频数 | 频率 |
1 |
| 70 | 0.35 |
2 |
| 10 | 0.05 |
3 |
| ① | 0.20 |
4 |
| 60 | 0.30 |
5 |
| 20 | ② |
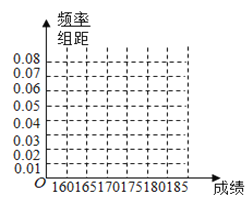
（1）请先求出频率分布表中①、②位置的相应数据，再完成频率分布直方图；
（2）为了能选拨出最优秀的学生，该校决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，求第3，4，5组各组抽取多少名学生进入第二轮面试；
（3）在（2）的前提下，从这6名学生中随机抽取2名学生进行外语交流面试，求这2名学生均来自同一组的概率.
