题目内容
在数列{an}中,“an=2an﹣1,n=2,3,4,…”是“{an}是公比为2的等比数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
若“{an}是公比为2的等比数列,
则当n≥2时,an=2an﹣1,成立.
当an=0,n=1,2,3,4,…时满足an=2an﹣1,n=2,3,4,但此时{an}不是等比数列,
∴“an=2an﹣1,n=2,3,4,…”是“{an}是公比为2的等比数列”的必要不充分条件.
故选:B.
则当n≥2时,an=2an﹣1,成立.
当an=0,n=1,2,3,4,…时满足an=2an﹣1,n=2,3,4,但此时{an}不是等比数列,
∴“an=2an﹣1,n=2,3,4,…”是“{an}是公比为2的等比数列”的必要不充分条件.
故选:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
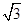 ,这个条件是其充分条件吗?为什么?
,这个条件是其充分条件吗?为什么?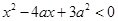 ,其中
,其中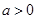 ,命题
,命题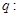 实数
实数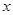 满足
满足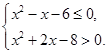 .
.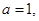 且
且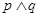 为真,求实数
为真,求实数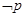 是
是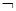
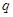 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.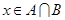 , 命题q:
, 命题q: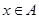 或
或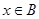 ,则
,则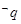 是
是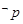 的( )
的( )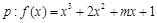 在(
在(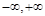 )上单调递增;
)上单调递增;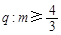 ,则p是q的( )
,则p是q的( )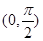 上为增函数”的 条件(在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中,选择适当的一种填空).
上为增函数”的 条件(在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中,选择适当的一种填空).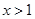 ”是“
”是“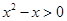 ”的 ( )
”的 ( )