题目内容
设命题 :函数
:函数 在
在 上单调递增;命题
上单调递增;命题 :不等式
:不等式
 对任意的
对任意的 恒成立.若“
恒成立.若“ 且
且 ”为假,“
”为假,“ 或
或 ”为真,求
”为真,求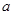 的取值范围.
的取值范围.
 :函数
:函数 在
在 上单调递增;命题
上单调递增;命题 :不等式
:不等式
 对任意的
对任意的 恒成立.若“
恒成立.若“ 且
且 ”为假,“
”为假,“ 或
或 ”为真,求
”为真,求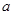 的取值范围.
的取值范围.
解:∵ 在
在 上单调递增 ∴
上单调递增 ∴
又不等式
 对任意的
对任意的 恒成立
恒成立
当 时,不等式可化为
时,不等式可化为 ,符合题意
,符合题意
当 时,
时,
 ∴
∴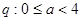
∵“ 且
且 ”为假,“
”为假,“ 或
或 ”为真 ∴
”为真 ∴ 、
、 中有且只有一个为真.
中有且只有一个为真.
⑴若“ 真
真 假”,则
假”,则

⑵若“ 假
假 真”,则
真”,则

综上,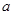 的取值范围是
的取值范围是 .
.
 在
在 上单调递增 ∴
上单调递增 ∴
又不等式

 对任意的
对任意的 恒成立
恒成立当
 时,不等式可化为
时,不等式可化为 ,符合题意
,符合题意当
 时,
时,
 ∴
∴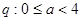
∵“
 且
且 ”为假,“
”为假,“ 或
或 ”为真 ∴
”为真 ∴ 、
、 中有且只有一个为真.
中有且只有一个为真.⑴若“
 真
真 假”,则
假”,则

⑵若“
 假
假 真”,则
真”,则

综上,
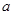 的取值范围是
的取值范围是 .
.
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 且
且 ,则
,则 是等差数列
是等差数列 项和为
项和为 ,且
,且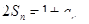 ,则数列
,则数列
 ,则
,则 ,则
,则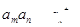




 :方程
:方程 是焦点在
是焦点在 轴上的椭圆,
轴上的椭圆, :函数
:函数 在
在 上单调递增,
上单调递增,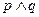 为假,
为假, 为真,求实数
为真,求实数 的取值范围.
的取值范围. 和平面
和平面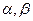 ,有以下四个命题:
,有以下四个命题: //
// ,
, //
//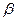 ,
,  //
//
 ,
, ,
,
 ,
, 
 =(a1,a2,a3),
=(a1,a2,a3), =(b1,b2,b3),给出下列三个命题:
=(b1,b2,b3),给出下列三个命题: ①
① =
= =
=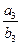 ②若a1=a2=a3=1,则
②若a1=a2=a3=1,则 ③
③ ,则动点P的轨迹为椭圆;②抛物线
,则动点P的轨迹为椭圆;②抛物线 的焦点坐标是
的焦点坐标是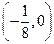 ;③“若q≤1,则x2+2x+q=0有实根”的逆否命题;④若点
;③“若q≤1,则x2+2x+q=0有实根”的逆否命题;④若点 到直线
到直线 的距离比它到点
的距离比它到点 的距离小1,则点
的距离小1,则点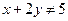 ,则
,则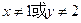 ”是______________命题(填真,假)
”是______________命题(填真,假) ②若
②若
 ④
④