题目内容
关于数列{an}有以下命题,其中错误的命题为 ( )
A.若 且 且 ,则 ,则 是等差数列 是等差数列 |
B.设数列 的前 的前 项和为 项和为 ,且 ,且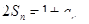 ,则数列 ,则数列 的通项 的通项 |
C.若 且 且 ,则 ,则 是等比数列 是等比数列 |
D.若 是等比数列,且 是等比数列,且 ,则 ,则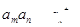 |
C
解:A、当n≥2时,由an+1+an-1=2an,变形得:an+1-an=an-an-1,根据等差数列的性质得到{an}是等差数列,本选项正确;
B、当n=1时,2S1=2a1=1+a1,解得a1=1,
n≥2时,由2Sn=1+an①得到:2Sn-1=1+an-1②,
①-②得:2an=an-an-1,即an=-an-1,即公比q=-1,
所以数列{an}为首项为1,公比为-1的等比数列,
则an=(-1)n-1,本选项正确;
C、当数列{an}的各项为0时,满足n≥2且an+1an-1=an2,但数列{an}不是等比数列,本选项错误;
D、因为{an}是等比数列,m,n,k∈N+,m+n=2k,所以根据等比数列的性质得到aman=ak2,本选项正确,
则错误的命题的选项为C.
故选C

练习册系列答案
相关题目
 在x∈R内单调递减;Q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点。如果
在x∈R内单调递减;Q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点。如果 为真,
为真, 也为真,求a的取值范围。
也为真,求a的取值范围。 :不等式
:不等式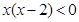 的解集是
的解集是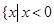 或
或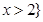 ,命题
,命题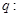 “在
“在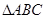 中,
中,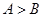 是
是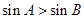 的充要条件”则( )
的充要条件”则( ) 假
假 真
真 假
假 :函数
:函数 在
在 上单调递增;命题
上单调递增;命题 :不等式
:不等式
 对任意的
对任意的 恒成立.若“
恒成立.若“ 的取值范围.
的取值范围. 按
按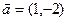 平移可得曲线
平移可得曲线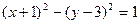 ;
; -1|+|
-1|+| -1|
-1|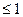 ,则使
,则使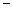
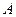 、
、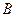 为两个定点,
为两个定点,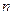 为
为 常数,
常数,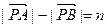 ,则动点
,则动点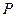 的轨迹为双曲线;
的轨迹为双曲线;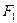 、
、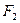 ,
,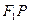 到点
到点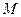 ,使
,使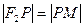 ,则点
,则点 (写出所有真命题的序号).
(写出所有真命题的序号). ②圆x2+y2+4x+2y+1=0与直线y=
②圆x2+y2+4x+2y+1=0与直线y=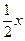 相交,所得弦长为2.
相交,所得弦长为2. +
+ )=
)=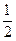 ,si
,si n(
n(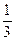 ,则tan
,则tan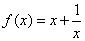 的值域是(-∞,-2]∪[2,+∞);
的值域是(-∞,-2]∪[2,+∞);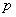 与命题
与命题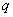 ,若
,若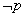 是
是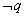 的充分不必要条件
的充分不必要条件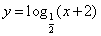 的图象经过第一象限;
的图象经过第一象限;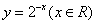 的反函数是
的反函数是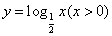 ;
;