题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(Ⅲ)求证:存在![]() ,当
,当![]() 时,
时, ![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)最小值为
(Ⅱ)最小值为![]() .(Ⅲ)详见解析
.(Ⅲ)详见解析
【解析】试题分析:(Ⅰ)求出导数,求得切线的斜率![]() ,所以
,所以![]() ,得
,得![]() .;
.;
(Ⅱ)![]() ,令
,令![]() ,得
,得![]() ,列表求得函数
,列表求得函数![]() 的最小值
的最小值
(Ⅲ)显然![]() ,且
,且![]() ,分析可知,
,分析可知, ![]() 存在两个零点,分别为
存在两个零点,分别为![]() ,
, ![]() .且
.且![]() 在
在![]() 上单调递增,
上单调递增, ![]() 在
在![]() 上单调递减,
上单调递减, ![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 是极大值,
是极大值, ![]() 是极小值,由题可得
是极小值,由题可得![]() ,进而
,进而![]() ,
,
因此![]() 时,
时, ![]() . 因为
. 因为![]() 且
且![]() 在
在![]() 上单调递增,
上单调递增,
所以一定存在![]() 满足
满足![]() ,所以存在
,所以存在![]() ,当
,当![]() 时,
时, ![]() .
.
试题解析:(Ⅰ) ![]() ,
,
由已知可得![]() ,所以
,所以![]() ,得
,得![]() .
.
(Ⅱ)![]() ,令
,令![]() ,得
,得![]() ,
,
所以![]() ,
, ![]() ,
, ![]() 的变化情况如表所示:
的变化情况如表所示:
|
|
|
|
|
|
|
|
| 极小值 |
|
所以![]() 的最小值为
的最小值为![]() .
.
(Ⅲ)证明:显然![]() ,且
,且![]() ,
,
由(Ⅱ)知, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又![]() ,
, ![]() ,
,
由零点存在性定理,存在唯一实数![]() ,满足
,满足![]() ,
,
即![]() ,
, ![]() ,
,
综上, ![]() 存在两个零点,分别为
存在两个零点,分别为![]() ,
, ![]() .
.
所以![]() 时,
时, ![]() ,即
,即![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
![]() 时,
时, ![]() ,即
,即![]() ,
, ![]() 在
在![]() 上单调递减;
上单调递减;
![]() 时,
时, ![]() ,即
,即![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 是极大值,
是极大值, ![]() 是极小值,
是极小值,
![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因此![]() 时,
时, ![]() .
.
因为![]() 且
且![]() 在
在![]() 上单调递增,
上单调递增,
所以一定存在![]() 满足
满足![]() ,
,
所以存在![]() ,当
,当![]() 时,
时, ![]() .
.

【题目】某种产品的以往各年的宣传费用支出![]() (万元)与销售量
(万元)与销售量![]() (万件)之间有如下对应数据
(万件)之间有如下对应数据
| 2 | 4 | 5 | 6 | 8 |
| 4 | 3 | 6 | 7 | 8 |
(1)试求回归直线方程;
(2)设该产品的单件售价与单件生产成本的差为![]() (元),若
(元),若![]() 与销售量
与销售量![]() (万件)的函数关系是
(万件)的函数关系是![]() ,试估计宣传费用支出
,试估计宣传费用支出![]() 为多少万元时,销售该产品的利润最大?(注:销售利润=销售额-生产成本-宣传费用)
为多少万元时,销售该产品的利润最大?(注:销售利润=销售额-生产成本-宣传费用)
(参考数据与公式: ![]() ,
, ![]() ,
, 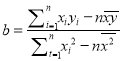 )
)
【题目】一企业从某条生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到如下的频率分布表:
x | [11,13) | [13,15) | [15,17) | [17,19) | [19,21) | [21,23) |
频数 | 2 | 12 | 34 | 38 | 10 | 4 |
(Ⅰ)作出样本的频率分布直方图,并估计该技术指标值x的平均数和众数;
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.



