题目内容
【题目】数列{an}满足
，则{an}的前60项和为（ ）
A. 3690 B. 3660 C. 1845 D. 1830
【答案】D
【解析】∵an+1+(-1)nan=2n-1,
∴当n=2k(k∈N*)时,a2k+1+a2k=4k-1①
当n=2k+1(k∈N)时,a2k+2-a2k+1=4k+1②
①+②得:a2k+a2k+2=8k.
则a2+a4+a6+a8+…+a60=(a2+a4)+(a6+a8)+…+(a58+a60)=8(1+3+…+29)=8×
=1800.
由②得a2k+1=a2k+2-(4k+1),
所以a1+a3+a5+…+a59=a2+a4+…+a60-[4×(0+1+2+…+29)+30]=1800-(4×
+30)=30,
∴a1+a2+…+a60=1800+30=1830.
练习册系列答案
相关题目
【题目】全世界越来越关注环境保护问题，某监测站点于2016年8月某日起连续
天监测空气质量指数
，数据统计如下：
空气质量指数 |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 |
|
|
|
|
|
（1）根据所给统计表和频率分布直方图中的信息求出
的值，并完成頻率分布直方图：
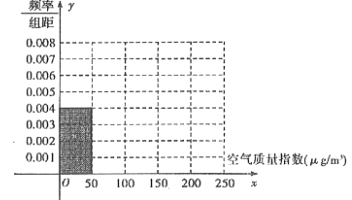
（2）由頻率分布直方图，求该组数据的平均数与中位数；
（3）在空气质量指数分别为
和
的监测数据中，用分层抽样的方法抽取
天，从中任意选取
天，求事件
“两天空气都为良”发生的概率.
