题目内容
17.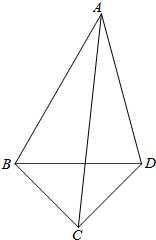 如图,在平面四边形ABCD中,AD=$\sqrt{6}$,CD=$\sqrt{2}$,∠ABD=60°,∠ADB=75°,
如图,在平面四边形ABCD中,AD=$\sqrt{6}$,CD=$\sqrt{2}$,∠ABD=60°,∠ADB=75°,∠ADC=120°.
(1)求BD的长;
(2)求△ABC的面积.
分析 (1)求出,∠ABD=60°,∠BAD=180°-60°-75°=45°,利用正弦定理,求BD的长;
(2)利用△ABD的面积+△BCD的面积-△ACD的面积,即可求△ABC的面积.
解答 解:(1)在△ABD中,AD=$\sqrt{6}$,∠ABD=60°,∠BAD=180°-60°-75°=45°,
由正弦定理得 $\frac{BD}{sin45°}$=$\frac{\sqrt{6}}{sin60°}$,所以BD=2.…(4分)
(2)在△ABD中,AD=$\sqrt{6}$,BD=2,∠ADB=75°,
所以△ABD的面积S1=$\frac{1}{2}$AD•BD•sin∠ADB=$\frac{3+\sqrt{3}}{2}$.…(8分)
又△ACD的面积S2=$\frac{1}{2}$AD•DC•sin∠ADC=$\frac{3}{2}$,…(10分)
△BCD的面积S3=1.…(12分)
所以△ABC的面积S=S1+S3-S2=$\frac{2+\sqrt{3}}{2}$.…(14分)
点评 本题考查正弦定理,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.如图,∠ACB=90°,CD⊥AB于点D,以BD为直径的圆与BC交于占E,则( )
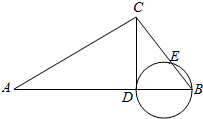

| A. | AD•AB=CD2 | B. | CE•CB=AD•AB | C. | CE•CB=AD•DB | D. | CE•EB=CD2 |
2.若q<19,则将(x-q)(x-q-1)(x-q-2)•…•(x-19)写成A${\;}_{n}^{m}$的形式是( )
| A. | A${\;}_{x-q}^{x-19}$ | B. | A${\;}_{x-q}^{x-20}$ | C. | A${\;}_{x-q}^{19-q}$ | D. | A${\;}_{x-q}^{20-q}$ |
9.设数列Sn是等差数列{an}的前n项和,若a3=5,a8=11,则S10=( )
| A. | 90 | B. | 80 | C. | 100 | D. | 120 |
6.若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为( )
| A. | 120° | B. | 150° | C. | 180° | D. | 240° |
7.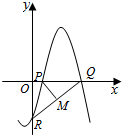 如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )
如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )
 如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )
如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )| A. | 2$\sqrt{3}$ | B. | $\frac{7\sqrt{3}}{3}$ | C. | $\frac{8\sqrt{3}}{3}$ | D. | 4$\sqrt{3}$ |