题目内容
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,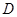 是AC的中点,已知
是AC的中点,已知 ,
,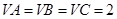 .
.
(1)求证:AC⊥平面VOD;
(2)求三棱锥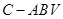 的体积.
的体积.
(1)证明见解析;(2) .
.
解析试题分析:(1)证明线面垂直,要证明直线与平面内的两条相交直线垂直,首先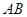 是圆
是圆 的直径,因此有
的直径,因此有 ,而
,而 分别是
分别是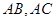 的中点,因此有
的中点,因此有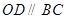 ,从而
,从而 ,再看已知条件
,再看已知条件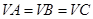 ,则点
,则点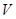 在平面
在平面 内的射影为
内的射影为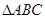 的外心,即点
的外心,即点 ,即
,即 平面
平面 ,从而有
,从而有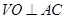 ,因此有
,因此有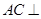 平面
平面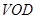 ;(2)棱锥
;(2)棱锥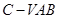 的体积,就是
的体积,就是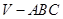 的体积,而棱锥
的体积,而棱锥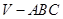 的高就是
的高就是
 ,底面是
,底面是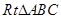 ,又
,又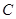 是弧
是弧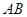 的中点,因此有
的中点,因此有 ,从而有
,从而有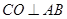 ,
,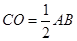 ,底面积、体积均可求.
,底面积、体积均可求.
(1)∵VA=VB,O为AB中点,∴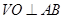 .
.
连接 ,在
,在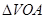 和
和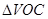 中,
中,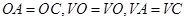 ,
,
∴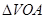 ≌DVOC ,∴
≌DVOC ,∴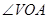 =ÐVOC=90°, ∴
=ÐVOC=90°, ∴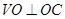
∵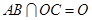 ,
, 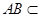 平面ABC,
平面ABC, 
 平面ABC, ∴VO⊥平面ABC.
平面ABC, ∴VO⊥平面ABC.
∵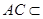 平面ABC,∴
平面ABC,∴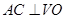 .
.
又∵ ,
,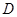 是
是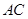 的中点,∴
的中点,∴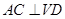 .
.
∵VOÌ平面VOD,VDÌ平面VOD, ,∴ AC
,∴ AC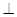 平面DOV.
平面DOV.
(2)由(2)知 是棱锥
是棱锥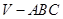 的高,且
的高,且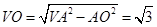 .
.
又∵点C是弧的中点,∴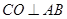 ,且
,且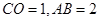 ,
,
∴三角形 的面积
的面积 ,
,
∴棱锥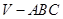 的体积为
的体积为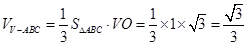
故棱锥 的体积为
的体积为 . 12分
. 12分
考点:线面垂直,棱锥的体积.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目


 ,BC=CD=2,
,BC=CD=2, .
.
 的棱长为2,E、F分别是
的棱长为2,E、F分别是 、
、 的中点,过
的中点,过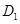 、E、F作平面
、E、F作平面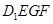 交
交 于G.
于G. ;
;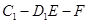 的余弦值;
的余弦值;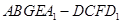 的体积.
的体积.
 的底面
的底面 是边长为
是边长为 的正方形,高
的正方形,高 ,
, 为
为 的中点,
的中点, 与
与 交于
交于 点.
点.  平面
平面 ;
; ∥平面
∥平面 ;
; 的体积.
的体积.
 ,M是线段AE上的动点.
,M是线段AE上的动点.
 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,
, ,
,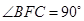 ,
, ,
, 是
是 的中点.
的中点.
 平面
平面 ;
; 平面
平面 ;
;
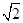 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.