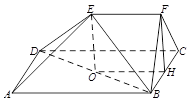
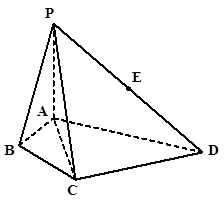题目内容
如图,在五面体 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,
, ,
, ,
,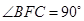 ,
, ,
, 是
是 的中点.
的中点.
(1)求证: 平面
平面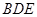 ;
;
(2)求证: 平面
平面 ;
;
(3)求五面体 的体积.
的体积.
(1)详见解析;(2)详见解析;(3) .
.
解析试题分析:(1)连接 交
交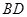 于点
于点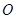 ,取
,取 的中点
的中点 ,连接
,连接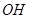 、
、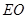 ,先证明
,先证明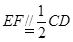 ,再利用中位线证明
,再利用中位线证明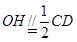 ,利用传递性证明
,利用传递性证明 ,进而证明四边形
,进而证明四边形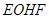 为平行四边形,进而得到
为平行四边形,进而得到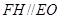 ,最后利用直线与平面平行的判定定理证明
,最后利用直线与平面平行的判定定理证明 平面
平面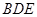 ;(2)证法一是取
;(2)证法一是取 的中点
的中点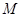 ,先证明四边形
,先证明四边形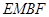 为平行四边形得到
为平行四边形得到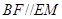 ,然后通过勾股定理证明
,然后通过勾股定理证明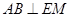 从而得到
从而得到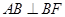 ,然后结合四边形
,然后结合四边形 为正方形得到
为正方形得到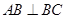 ,最后利用直线与平面垂直的判定定理证明
,最后利用直线与平面垂直的判定定理证明 平面
平面 ;证法二是连接
;证法二是连接 交
交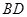 于点
于点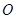 ,先利用勾股定理证明
,先利用勾股定理证明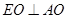 ,利用
,利用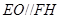 得到
得到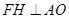 ,再利用等腰三角形
,再利用等腰三角形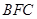 中三线合一得到
中三线合一得到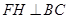 ,利用直线与平面垂直的判定定理证明
,利用直线与平面垂直的判定定理证明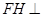 平面
平面 ,进而得到
,进而得到 ,然后结合四边形
,然后结合四边形 为正方形得到
为正方形得到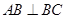 ,最后利用直线与平面垂直的判定定理证明
,最后利用直线与平面垂直的判定定理证明 平面
平面 ;(3)将五面体分割为四棱锥
;(3)将五面体分割为四棱锥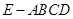 与三棱锥
与三棱锥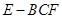 ,利用(2)中的结论
,利用(2)中的结论 平面
平面 得到
得到 平面
平面 从而计算三棱锥
从而计算三棱锥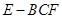 的体积,利用结论
的体积,利用结论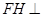 平面
平面 以及
以及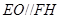 得到
得到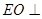 平面
平面 以此计算四棱锥
以此计算四棱锥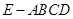 的体积,最终将两个锥体的体积相加得到五面体
的体积,最终将两个锥体的体积相加得到五面体 的体积.
的体积.
试题解析:(1)连接 ,
, 与
与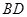 相交于点
相交于点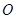 ,则
,则 是
是 的中点,连接
的中点,连接 、
、 ,
,
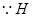 是
是 的中点,
的中点,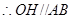 ,
, ,
,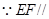 平面
平面 ,
,
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ,其表面展开图是三角形
,其表面展开图是三角形 ,如图,求△
,如图,求△ .
.
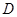 是AC的中点,已知
是AC的中点,已知 ,
,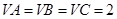 .
.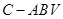 的体积.
的体积.
 的正三棱锥
的正三棱锥 中,
中, 长为
长为 ,
,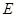 为棱
为棱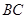 的中点,求
的中点,求
 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
 求三棱锥B1-A1DC的体积.
求三棱锥B1-A1DC的体积.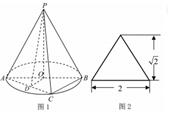
 平面POD;
平面POD; ,在三棱锥A-PBC中,求点A到平面PBC的距离.
,在三棱锥A-PBC中,求点A到平面PBC的距离. ,
,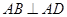 ,
,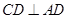 ,
,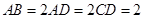 沿
沿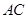 折叠成三棱锥,当三棱锥体积最大时,求此时三棱锥外接球的体积
折叠成三棱锥,当三棱锥体积最大时,求此时三棱锥外接球的体积