题目内容
已知一圆C的圆心为(2,-1),且该圆被直线l:x-y-1=0截得的弦长为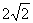 ,求该圆的方程及过弦的两端点的切线方程.
,求该圆的方程及过弦的两端点的切线方程.
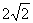 ,求该圆的方程及过弦的两端点的切线方程.
,求该圆的方程及过弦的两端点的切线方程. 过弦两端点的该圆的切线方程是x=0和y=1
设圆C的方程是(x-2)2+(y+1)2=r2(r>0),则弦长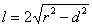 ,其中d为圆心到直线x-y-1=0的距离,
,其中d为圆心到直线x-y-1=0的距离, .
.
∴
∴r2=4.
∴圆的方程为(x-2)2+(y+1)2=4.
由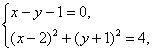 解得弦的两端点坐标是(2,1)和(0,-1).
解得弦的两端点坐标是(2,1)和(0,-1).
∴过弦两端点的该圆的切线方程是x=0和y=1.
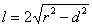 ,其中d为圆心到直线x-y-1=0的距离,
,其中d为圆心到直线x-y-1=0的距离, .
.∴

∴r2=4.
∴圆的方程为(x-2)2+(y+1)2=4.
由
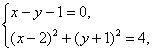 解得弦的两端点坐标是(2,1)和(0,-1).
解得弦的两端点坐标是(2,1)和(0,-1).∴过弦两端点的该圆的切线方程是x=0和y=1.

练习册系列答案
相关题目
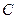
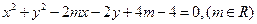
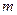 的值,使圆
的值,使圆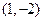 的直线方程.
的直线方程. 取最大值时,点P的横坐标为_______________。
取最大值时,点P的横坐标为_______________。
 交于A、B两点,O是坐标原点,向量
交于A、B两点,O是坐标原点,向量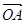 、
、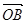 满足
满足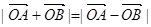 ,则实数a的值是( )
,则实数a的值是( )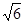 或-
或-