Question

【题目】在平面直角坐标系中，点， ，动点满足.

（1）求动点的轨迹的方程；

（2）若直线与轨迹有且仅有一个公共点，且与直线相交于点，求证：以为直径的圆过定点.

Answer 1

【答案】（1）；（2）见解析.

【解析】试题分析：（1）利用椭圆的定义判定轨迹为椭圆，并求出，a,b,从而写出标准方程；（2）以为直径的圆过定点可转化为，利用向量可比较容易证明,先联立方程，消元得，可得， ，从而， ，根据数量积为0即可证明.

试题解析：

（1）解：因为

即

由椭圆定义可知动点的轨迹是以为焦点的椭圆

所以，

所以椭圆的方程为.

（2）证明：由，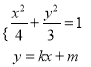

消去得

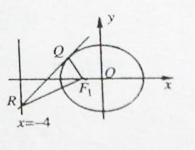
如图，设点，依题意，

∵直线与轨迹有且仅有一个公共点

∴由，

可得.

此时， ，即， ，

∴，

由，解得

∴

由

可得，

∴

∴

∴以为直径的圆过定点.