题目内容
【题目】设![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .关于函数
.关于函数![]() 的零点,有下列三个命题:
的零点,有下列三个命题:
①当![]() 时,存在实数m,使函数
时,存在实数m,使函数![]() 恰有5个不同的零点;
恰有5个不同的零点;
②若![]() ,函数
,函数![]() 的零点不超过4个,则
的零点不超过4个,则![]() ;
;
③对![]() ,
,![]() ,函数
,函数![]() 恰有4个不同的零点,且这4个零点可以组成等差数列.
恰有4个不同的零点,且这4个零点可以组成等差数列.
其中,正确命题的序号是_______.
【答案】①②③
【解析】
根据偶函数的图象关于![]() 轴对称,利用已知中的条件作出偶函数的图象,利用图象对各个选项进行判断即可.
轴对称,利用已知中的条件作出偶函数的图象,利用图象对各个选项进行判断即可.
解:当![]() 时
时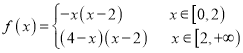 又因为
又因为![]() 为偶函数
为偶函数
![]() 可画出
可画出![]() 的图象,如下所示:
的图象,如下所示:
可知当![]() 时
时![]() 有5个不同的零点;故①正确;
有5个不同的零点;故①正确;
若![]() ,函数
,函数![]() 的零点不超过4个,
的零点不超过4个,
即![]() ,
,![]() 与
与![]() 的交点不超过4个,
的交点不超过4个,
![]() 时
时![]() 恒成立
恒成立
又![]() 当
当![]() 时,
时,![]()
![]() 在
在![]() 上恒成立
上恒成立
![]() 在
在![]() 上恒成立
上恒成立
![]()
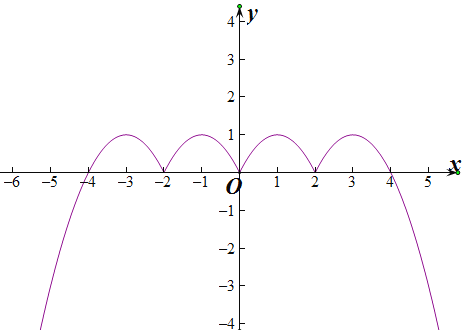
由于偶函数![]() 的图象,如下所示:
的图象,如下所示:
直线![]() 与图象的公共点不超过
与图象的公共点不超过![]() 个,则
个,则![]() ,故②正确;
,故②正确;
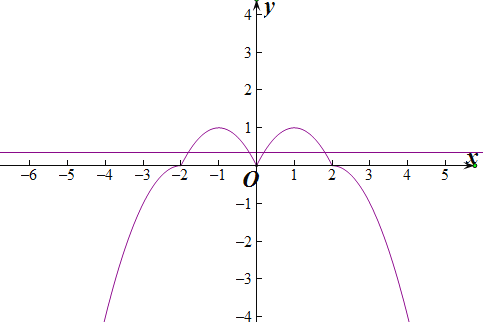
对![]() ,偶函数
,偶函数![]() 的图象,如下所示:
的图象,如下所示:
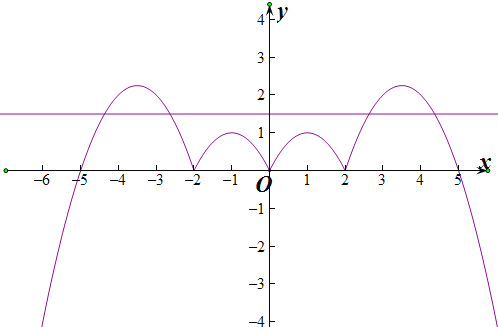
![]() ,使得直线
,使得直线![]() 与
与![]() 恰有4个不同的交点点,且相邻点之间的距离相等,故③正确.
恰有4个不同的交点点,且相邻点之间的距离相等,故③正确.
故答案为:①②③

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) |
|
|
|
从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图:
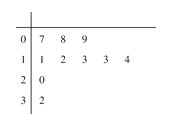
(Ⅰ)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数X的分布列与数学期望;
(Ⅱ)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到![]() 户月用水量为一阶的可能性最大,求
户月用水量为一阶的可能性最大,求![]() 的值.
的值.