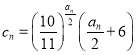题目内容
【题目】在单位正![]() 内任取一点P,以PA、PB、PC为边生成
内任取一点P,以PA、PB、PC为边生成![]() .
.
(1)当![]() 分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
(2)证明:当![]() 的周长取最小值时,面积取最大值.
的周长取最小值时,面积取最大值.
【答案】(1)见解析;(2)![]()
【解析】
如图,记![]() .
.
将![]() 绕点B逆时针旋转
绕点B逆时针旋转![]() 得
得![]() ,则
,则![]() ,
,![]() .
.![]() 就是由PA、PB、PC所组成的
就是由PA、PB、PC所组成的![]() ,且其三个内角
,且其三个内角![]() ,
,![]() ,
,![]() .
.

(1)当存在![]() 时,
时,![]() 为直角三角形.
为直角三角形.
由![]() ,知
,知![]() .
.
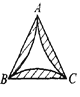
所以,点P在三个单位圆的![]() 弧AB、BC、CA上(图).
弧AB、BC、CA上(图).
当存在![]() 时,
时,![]() 为钝角三角形.
为钝角三角形.
由![]() ,知
,知![]() .
.
由圆内角大于圆周角知,点P在图中的三个弓形内(阴影部分,不包括边界).
当![]() ,
,![]() ,
,![]() 同时成立时,
同时成立时,![]() 为锐角三角形,得
为锐角三角形,得![]() ,
,![]() ,
,![]() .
.
由圆外角小于圆周角知,点P在图8中的三个圆弧外(曲边![]() 内部,不包括边界).
内部,不包括边界).
(2)先确定![]() 周长取最小值时点P的位置.为此,将如图的
周长取最小值时点P的位置.为此,将如图的![]() 绕点B逆时针旋转
绕点B逆时针旋转![]() 得
得![]() ,联结MC、PN.则折线
,联结MC、PN.则折线![]() .
.
当且仅当M、N、P、C四点共线时,![]() 的周长取最小值.此时,有
的周长取最小值.此时,有![]() ,即点P为
,即点P为![]() 的中心(
的中心(![]() ).
).
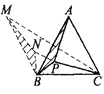
下面说明,这恰好是面积取最大值的条件.
在![]() 中,由余弦定理和基本不等式有
中,由余弦定理和基本不等式有![]() ,
,
故![]() .当且仅当
.当且仅当![]() 时,等号成立.
时,等号成立.
在![]() 中,
中,![]() .
.
由面积公式有![]()
![]()

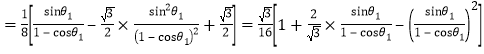
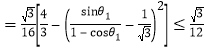 .
.
两处放大的地方同时取等号当且仅当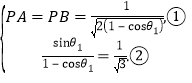
由式②有![]() .
.
所以,![]() .
.
从而,![]() ,代入式①得
,代入式①得![]() .
.
这表明,PA、PB在![]() 的中线上,且相交于距顶点
的中线上,且相交于距顶点![]() 处,点P为中心.
处,点P为中心.
所以,当点P为![]() 的中心时,
的中心时,![]() 的周长最短且面积最大,最大值为
的周长最短且面积最大,最大值为![]() .
.

练习册系列答案
相关题目
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: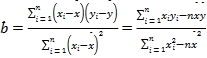 ,
,![]() .
.