题目内容
【题目】已知函数![]() . 设关于
. 设关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,若
,若![]() ,则实数
,则实数![]() 的取值范围是___.
的取值范围是___.
【答案】![]()
【解析】
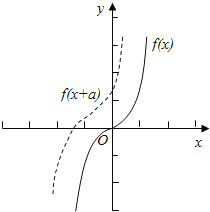
由题意可得,在[![]() ,
,![]() ]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.当a=0或 a>0时,检验不满足条件.当a<0时,应有f(
]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.当a=0或 a>0时,检验不满足条件.当a<0时,应有f(![]() a)<f(
a)<f(![]() ),化简可得 a2﹣a﹣1<0,由此求得a的范围.
),化简可得 a2﹣a﹣1<0,由此求得a的范围.
由于f(x)![]() ,
,
关于x的不等式f(x+a)<f(x)的解集为M,若[![]() ,
,![]() ]A,
]A,
则在[![]() ,
,![]() ]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.
]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.
当a=0时,显然不满足条件.
当a>0时,函数y=f(x+a)的图象是把函数y=f(x)的图象向左平移a个单位得到的,
结合图象(右上方)可得不满足函数y=f(x+a)的图象在函数y=f(x)的图象下方.
当a<0时,如图所示,要使在[![]() ,
,![]() ]上,
]上,
函数y=f(x+a)的图象在函数y=f(x)的图象的下方,
只要f(![]() a)<f(
a)<f(![]() )即可,
)即可,
即﹣a(![]() a)2+(
a)2+(![]() a)<﹣a(
a)<﹣a(![]() )2
)2![]() ,
,
化简可得 a2﹣a﹣1<0,解得 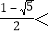 a
a![]() ,
,
故此时a的范围为(![]() ,0).
,0).
综上可得,a的范围为(![]() ,0),
,0),
故答案为:(![]() ,0).
,0).

【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
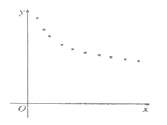
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作价格
哪一个更适宜作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() (
(![]() ),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为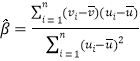 ,
,![]() .
.
【题目】随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.下表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.
成绩优秀 | 成绩不够优秀 | 总计 | |
选修生涯规划课 | 15 | 10 | 25 |
不选修生涯规划课 | 6 | 19 | 25 |
总计 | 21 | 29 | 50 |
(Ⅰ)根据列联表运用独立性检验的思想方法能否有![]() 的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
(Ⅱ)如果从全校选修生涯规划课的学生中随机地抽取3名学生,求抽到成绩不够优秀的学生人数![]() 的分布列和数学期望(将频率当作概率计算).
的分布列和数学期望(将频率当作概率计算).
参考附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式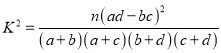 ,其中
,其中![]() .
.