Question

【题目】如图，在四棱锥P—ABCD中，底面ABCD为正方形，PA⊥底面ABCD，PA＝AD．M，N分别是AB，PC的中点．

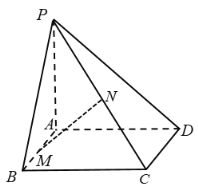
（1）求证：MN//平面PAD；

（2）求证：MN⊥平面PCD；

（3）求二面角B—PC—D的大小．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）120°．

【解析】

（1）取PD中点Q，连接NQ，AQ，则四边形MNQA是平行四边形，从而得到MN//AQ，由线面平行判定定理得MN//平面PAD；

（2）先证得AQ⊥平面PDC，由（1）得MN//AQ，从而得MN⊥平面PCD；

（3）过B作BH⊥PC于H，连接HD，BD.由已知条件得△PBC≌△PDC，从而得DH⊥PC，进而得∠BHD是二面角B—PC—D的平面角，在中，利用余弦定理求得∠BHD即可.

（1）证明：取PD中点Q，连接AQ，NQ，在△PCD中， N，Q分別为PC，PD的中点，

所以NQ//CD，且NQ＝CD，因为底面ABCD是正方形，且M为AB中点，所以AM//CD，且AM＝CD，

所以AM//NQ，且AM＝NQ，所以四边形AMNQ是平行四边形，所以MN//AQ，

又因为AQ平面PAD，MN平面PAD，所以MN//平面PAD.

（2）证明：因为底面ABCD是正方形，所以CD⊥AD，且PA⊥底面ABCD，CD平面ABCD，所以PA⊥CD，

又因为AD平面PAD，PA平面PAD，ADPA＝A，所以CD⊥平面PAD，

因为AQ平面PAD，所以CD⊥AQ，因为PA＝AD，Q是PD中点，所以AQ⊥PD，

又因为CD平面PCD，PD平面PCD，CDPD＝D，所以AQ⊥平面PCD.

由（1）得MN//AQ，所以MN⊥平面PCD.

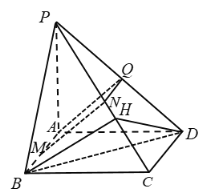
（3）过B作BH⊥PC于H，连接HD，BD，因为PA⊥底面ABCD，底面ABCD是正方形，且PA＝AD，

设PA＝AD＝a，则PB＝PD＝a，又因为CB＝CD＝a，PC＝PC，所以△PBC≌△PDC，

因为BH⊥PC，所以DH⊥PC，所以∠BHD是二面角B—PC—D的平面角.

由（2）CD⊥平面PAD，又为PD平面PAD，所以CD⊥PD，所以BH＝HD＝，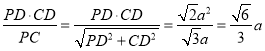

在中，，所以∠BHD＝120°，

所以二面角B—PC—D的大小为120°．