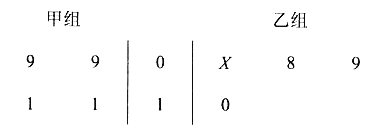Question

【题目】函数y=ex﹣mx在区间（0，3]上有两个零点，则m的取值范围是 ．

Answer 1

【答案】e＜m≤
【解析】解：由y=ex﹣mx=0得m= ，
设f（x）= ，
则f'（x）= ，
由f'（x）＞0，解得1＜x≤3，此时函数单调递增，
由f'（x）＜0，解得0＜x＜1，此时函数单调递减，
∴当x=1时，函数f（x）取得极小值，同时也是最小值f（1）=e，
∵当x→0时，f（x）→+∞，
当x=3时，f（3）= ，
∴要使函数y=ex﹣mx在区间（0，3]上有两个零点，
则e＜m≤ ，
所以答案是：e＜m≤ ．

【考点精析】本题主要考查了函数的零点的相关知识点，需要掌握函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点才能正确解答此题．