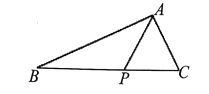
题目内容
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且cos2 ![]() ﹣sinBsinC=
﹣sinBsinC= ![]() .
.
(1)求A;
(2)若a=4,求△ABC面积的最大值.
【答案】
(1)解:在△ABC中,∵cos2 ![]() ﹣sinBsinC=
﹣sinBsinC= ![]() ,
,
∴ ![]() cos(B﹣C)﹣sinBsinC=
cos(B﹣C)﹣sinBsinC= ![]() ,
,
∴cos(B+C)=﹣ ![]() ,
,
∴cosA= ![]() ,
,
∵0<A<π,
∴A= ![]()
(2)解:由余弦定理可得16=b2+c2﹣ ![]() bc≥(2﹣
bc≥(2﹣ ![]() )bc,当且仅当b=c时取等号,
)bc,当且仅当b=c时取等号,
∴bc≤16+8 ![]() ,
,
∴S△ABC= ![]() =
= ![]() bc≤4(
bc≤4( ![]() +1),
+1),
∴△ABC面积的最大值为4( ![]() +1)
+1)
【解析】(1)利用二倍角公式,结合差、和角的余弦公式,即可求A;(2)若a=4,利用余弦定理,结合基本不等式,三角形的面积公式,即可求△ABC面积的最大值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目