题目内容
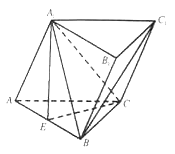
【题目】如图所示,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为矩形,
为矩形, ![]() ,点
,点![]() 为
为![]() 的中点.
的中点.

(1)证明: ![]() 平面
平面![]() .
.
(2)点![]() 为
为![]() 上任意一点,在线段
上任意一点,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,确定点
?若存在,确定点![]() 的位置,并加以证明;若不存在,请说明理由.
的位置,并加以证明;若不存在,请说明理由.
【答案】(1)见解析;(2)中点
【解析】试题分析:
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,利用
,利用![]() 是矩形得到
是矩形得到![]() ,再由线面平行的判定定理可证;
,再由线面平行的判定定理可证;
(2)当![]() 为
为![]() 中点时,有
中点时,有![]() ;取
;取![]() 中点
中点![]() ,连接
,连接![]() ,结合三角形的中位线性质以及面面平行的性质进行推理得到
,结合三角形的中位线性质以及面面平行的性质进行推理得到![]() 平面
平面![]() 即可.
即可.
试题解析:
(1)证明 连接AC交BD于O,连接OF,如图①.
∵四边形ABCD是矩形,∴O为AC的中点,又F为EC的中点,
∴OF为△ACE的中位线,:∴OF∥AE,又OF平面BDF,
AE平面BDF,∴AE∥平面BDF.
(2)当P为AE中点时,有PM⊥BE,
证明如下:取BE中点H,连接DP,PH,CH,
如图
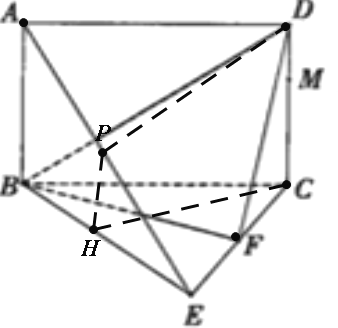
∵P为AE的中点,H为BE的中点,
∴PH∥AB,又AB∥CD,∴PH∥CD,
∴P,H,C,D四点共面.
∵平面ABCD∥平面BCE,CD⊥BC
∴CD⊥平面BCE,又BE平面BCE,
∴CD⊥BE∵BC=CE,H为BE的中点,
∴CH⊥BE,
∴BE⊥平面DPHC,又PM平面DPHC,
∴BE⊥PM即PM⊥BE

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目