题目内容
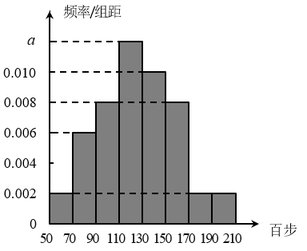
【题目】根据幼儿身心发展的特征,幼儿园通常着重在健康、科学、社会、语言、艺术五大领域对幼儿展开全方位的教育和培养.经调查发现,一个幼儿除了在幼儿园进行五大领域的系统学习之外,还会报一些课外兴趣班.而家长朋友们对于是否额外报这些课外兴趣班的态度也是不一样的.某调查机构对某幼儿园的100名幼儿家长就孩子是否报课外兴趣班的赞同程度进行调查统计,得到家长对幼儿报课外兴趣班赞同度![]() 的频数分布表:
的频数分布表:
赞同度 |
|
|
|
|
|
家长数 | 2 | 12 | 14 | 28 | 44 |
(1)分别计算对幼儿报兴趣班的赞同度不低于![]() 的家长比例和对幼儿报兴趣班的赞同度低于
的家长比例和对幼儿报兴趣班的赞同度低于![]() 的家长比例;
的家长比例;
(2)求家长对幼儿报兴趣班的赞同度的平均数与方差的估计值.(同一组中的数据用该组区间的中点值代替)
【答案】(1)![]() ,
,![]() ; (2)
; (2)![]() ,
,![]() .
.
【解析】
(1)直接利用频数分布表计算得到答案.
(2)直接利用平均值和方差的公式代入数据计算得到答案.
(1)根据家长对幼儿报课外兴趣班赞同度![]() 的频数分布表,
的频数分布表,
对幼儿报兴趣班的赞同度不低于![]() 的家长比例为
的家长比例为![]() ;
;
对幼儿报兴趣班的赞同度低于![]() 的家长比例为
的家长比例为![]() .
.
(2)由题意,家长对幼儿报兴趣班的赞同度的平均数为
![]()
![]() ,
,
其方差为
![]()
![]() ,
,
所以家长对幼儿报兴趣班的赞同度的平均数与方差的估计值分别为0.70和0.0496.

【题目】某公司有1000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族",计划在明年及明年以后才购买5G手机的员工称为“观望者”,调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
(1)完成下列![]() 列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
属于“追光族" | 属于“观望者" | 合计 | |
女性员工 | |||
男性员工 | |||
合计 | 100 |
(2)已知被抽取的这100名员工中有10名是人事部的员工,这10名中有3名属于“追光族”.现从这10名中随机抽取3名,记被抽取的3名中属于“追光族”的人数为随机变量X,求![]() 的分布列及数学期望.
的分布列及数学期望.
附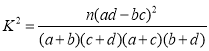 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | p>0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某学校为了解学生假期参与志愿服务活动的情况,随机调查了![]() 名男生,
名男生,![]() 名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
超过 | 不超过 | |
男 |
|
|
女 |
|
|
(1)能否有![]() 的把握认为该校学生一周参与志愿服务活动时间是否超过
的把握认为该校学生一周参与志愿服务活动时间是否超过![]() 小时与性别有关?
小时与性别有关?
(2)以这![]() 名学生参与志愿服务活动时间超过
名学生参与志愿服务活动时间超过![]() 小时的频率作为该事件发生的概率,现从该校学生中随机抽查
小时的频率作为该事件发生的概率,现从该校学生中随机抽查![]() 名学生,试估计这
名学生,试估计这![]() 名学生中一周参与志愿服务活动时间超过
名学生中一周参与志愿服务活动时间超过![]() 小时的人数.
小时的人数.
附:
|
|
|
|
|
|
|
|
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: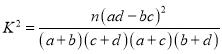
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |