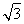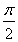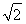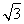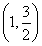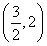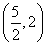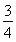题目内容
已知a>0,函数f(x)=ax2-ln x.
(1)求f(x)的单调区间;
(2)当a=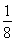 时,证明:方程f(x)=f
时,证明:方程f(x)=f 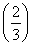 在区间(2,+∞)上有唯一解.
在区间(2,+∞)上有唯一解.
(1)单调递减区间为 ,单调递增区间为
,单调递增区间为 (2)见解析
(2)见解析
【解析】(1)函数f(x)的定义域为(0,+∞),f′(x)=2ax- =
=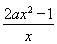 .
.
∵a>0,令f′(x)>0得x>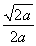 ;令f′(x)<0,得0<x<
;令f′(x)<0,得0<x<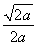 ,
,
∴函数f(x)的单调递减区间为 ,单调递增区间为
,单调递增区间为 .
.
(2)证明:当a=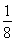 时,f(x)=
时,f(x)=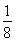 x2-ln x,由(1)知f(x)的单调递减区间为(0,2),单调递增区间为(2,+∞),
x2-ln x,由(1)知f(x)的单调递减区间为(0,2),单调递增区间为(2,+∞),
令g(x)=f(x)-f 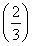 ,则g(x)在区间(2,+∞)单调递增且g(2)=f(2)-f
,则g(x)在区间(2,+∞)单调递增且g(2)=f(2)-f  <0,g(e2)=
<0,g(e2)=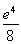 -2-
-2-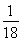 +ln
+ln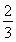 >0,
>0,
故方程f(x)=f 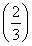 在区间(2,+∞)上有唯一解.
在区间(2,+∞)上有唯一解.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目