题目内容
已知某随机变量X的概率密度函数为P(x)= 则随机变量X落在区间(1,2)内的概率为( )
则随机变量X落在区间(1,2)内的概率为( )
A.e2+e B. C.e2-e D.
C.e2-e D. 
D
【解析】概率值为 =[-e-x]
=[-e-x]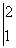 =e-1-e-2=
=e-1-e-2=

练习册系列答案
相关题目
题目内容
已知某随机变量X的概率密度函数为P(x)= 则随机变量X落在区间(1,2)内的概率为( )
则随机变量X落在区间(1,2)内的概率为( )
A.e2+e B. C.e2-e D.
C.e2-e D. 
D
【解析】概率值为 =[-e-x]
=[-e-x]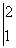 =e-1-e-2=
=e-1-e-2=
