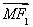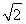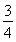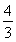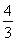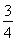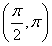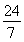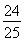题目内容
已知函数f(x)=2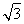 sin xcos x+2cos2x+m在区间
sin xcos x+2cos2x+m在区间 上的最大值为2.
上的最大值为2.
(1)求常数m的值;
(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,若f(A)=1,sin B=3sin C,△ABC的面积为 ,求边长a.
,求边长a.
(1)m=-1.(2)a=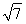
【解析】(1)f(x)=2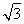 sin x·cos x+2cos2x+m=2sin(2x+
sin x·cos x+2cos2x+m=2sin(2x+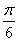 )+m+1.
)+m+1.
因为x∈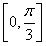 ,所以2x+
,所以2x+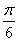 ∈
∈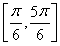 .
.
因为函数y=sin t在区间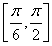 上是增函数,在区间
上是增函数,在区间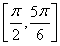 上是减函数,
上是减函数,
所以当2x+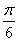 =
=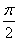 ,即x=
,即x=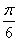 时,函数f(x)在区间
时,函数f(x)在区间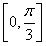 上取到最大值.此时,f(x)max=f
上取到最大值.此时,f(x)max=f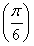 =m+3=2,得m=-1.
=m+3=2,得m=-1.
(2)因为f(A)=1,所以2sin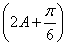 =1,
=1,
即sin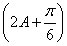 =
=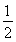 ,解得A=0(舍去)或A=
,解得A=0(舍去)或A=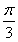 .
.
因为sin B=3sin C,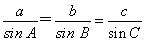 ,所以b=3c.①
,所以b=3c.①
因为△ABC的面积为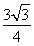 ,所以S△ABC=
,所以S△ABC=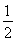 bcsin A=
bcsin A=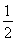 bcsin
bcsin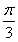 =
=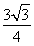 ,即bc=3.②
,即bc=3.②
由①和②解得b=3,c=1.
因为a2=b2+c2-2bc·cos A=32+12-2×3×1×cos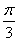 ,
,
所以a=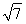

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目