题目内容
(本题满分14分)
已知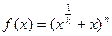 ,且正整数n满足
,且正整数n满足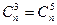 ,
,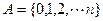
(1)求n ;
(2)若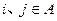 ,是否存在
,是否存在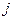 ,当
,当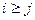 时,
时,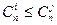 恒成立。若存在,求出最小的
恒成立。若存在,求出最小的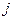 ;
;
若不存在,试说明理由。
(3)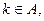 若
若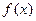 的展开式有且只有三个有理项,求
的展开式有且只有三个有理项,求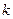 。
。
已知
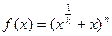 ,且正整数n满足
,且正整数n满足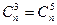 ,
,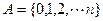
(1)求n ;
(2)若
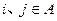 ,是否存在
,是否存在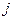 ,当
,当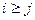 时,
时,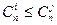 恒成立。若存在,求出最小的
恒成立。若存在,求出最小的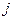 ;
;若不存在,试说明理由。
(3)
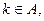 若
若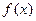 的展开式有且只有三个有理项,求
的展开式有且只有三个有理项,求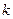 。
。解:(1)n="8 " 、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、4分
(2)存在最大二项式 系数满足条件,∴j=4、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、8分
系数满足条件,∴j=4、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、8分
(3)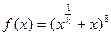 展开式通项为
展开式通项为 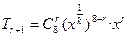 =
=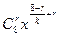
依题意,只须8-r是k的整数倍的r有且只有三个
分别令k=1,2,3……8,检验得k=3或4、、、、、、、、、、、、、、、、、、、、、、、、14
(2)存在最大二项式
 系数满足条件,∴j=4、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、8分
系数满足条件,∴j=4、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、8分(3)
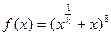 展开式通项为
展开式通项为 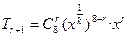 =
=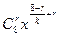
依题意,只须8-r是k的整数倍的r有且只有三个
分别令k=1,2,3……8,检验得k=3或4、、、、、、、、、、、、、、、、、、、、、、、、14
略

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 题14分)已知函数
题14分)已知函数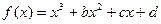 的图像过点
的图像过点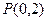 ,且在点
,且在点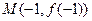 处的切线方程为
处的切线方程为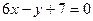 ,
,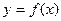 的解析式 ;
的解析式 ; 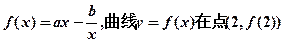 处的切线方程为
处的切线方程为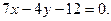
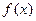 的解析式;
的解析式;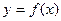 上任一
上任一 点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.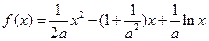 ,
,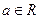
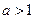 时,求
时,求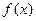 的单调区间;
的单调区间;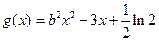 ,当
,当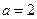 ,
,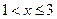 时,
时,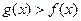 恒有解,求
恒有解,求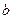 的取值范围.
的取值范围. ,则此函数图象在点(1,
,则此函数图象在点(1,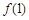 )处的切线的倾斜角为
)处的切线的倾斜角为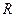 上的函数
上的函数 其中
其中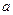 为常数。
为常数。 是函数
是函数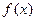 的一个极值点,求
的一个极值点,求 上为增函数,求
上为增函数,求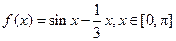 ,
,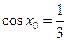 (
(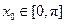 ).那么下面命题中真命题的序号是
).那么下面命题中真命题的序号是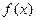 的最大值为
的最大值为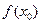 ②
② 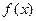 在
在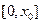 上是减函数 ④
上是减函数 ④ 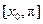 上是减函数
上是减函数 ②④
②④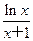 在点(1,0)处的切线与直线x-ay+1=0垂直,则a=
在点(1,0)处的切线与直线x-ay+1=0垂直,则a=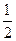
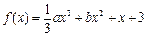 ,其中
,其中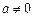 ..
..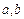 满足什么条件时,
满足什么条件时,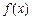 取得极值?
取得极值?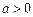 ,且
,且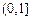 上单调递增,试用
上单调递增,试用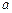 表示出
表示出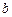 的取值范围.
的取值范围.