题目内容
.已知 ,则此函数图象在点(1,
,则此函数图象在点(1,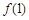 )处的切线的倾斜角为
)处的切线的倾斜角为
 ,则此函数图象在点(1,
,则此函数图象在点(1,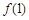 )处的切线的倾斜角为
)处的切线的倾斜角为| A.零角 | B.锐角 | C.直角 | D.钝角 |
D
分析:先求函数f(x)=excosx的导数,因为函数图象在点(1,f(1))处的切线的斜率为函数在x=1处的导数,就可求出切线的斜率,再根据切线的斜率是倾斜角的正切值,就可根据斜率的正负判断倾斜角是锐角还是钝角.
解:∵f′(x)=excosx-exsinx,∴f′(1)=e(cos1-sin1)
∴函数图象在点(1,f(1))处的切线的斜率为e(cos1-sin1)
∵e(cos1-sin1)<0,∴函数图象在点(1,f(1))处的切线的倾斜角为钝角
故选D

练习册系列答案
相关题目
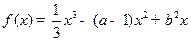 ,其中
,其中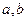 为常数.
为常数.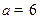 ,
,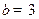 时,求函数
时,求函数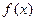 的单调递增区间;
的单调递增区间;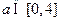 ,
,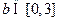 ,求函数
,求函数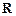 上是增函数的概率.
上是增函数的概率.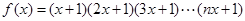 ,则
,则 ( )
( )
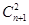
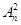

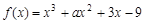 ,已知
,已知 在
在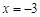 时取极值,则a=
时取极值,则a=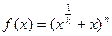 ,且正整数n满足
,且正整数n满足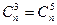 ,
,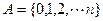
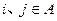 ,是否存在
,是否存在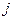 ,当
,当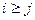 时,
时,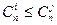 恒成立。若存在,求出最小的
恒成立。若存在,求出最小的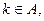 若
若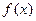 的展开式有且只有三个有理项,求
的展开式有且只有三个有理项,求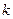 。
。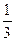 x3+
x3+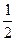 ax2+ax-2(a∈R),
ax2+ax-2(a∈R),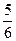 ,求实数a的取值范围.
,求实数a的取值范围.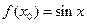 ,
,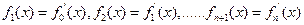
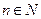 ,则
,则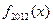 等于( )
等于( ) x
x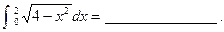
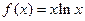 ,若
,若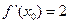 ,则
,则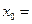 ____________.
____________.