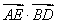题目内容
已知△ABC的内角A,B,C所对的边分别是a,b,c,设向量m=(a,b),n=(sin B,sin A),p=(b-2,a-2).
(1)若m∥n,求证:△ABC为等腰三角形;
(2)若m⊥p,边长c=2,C=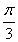 ,求△ABC的面积.
,求△ABC的面积.
(1)见解析(2)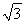
【解析】(1)因为m∥n,所以asin A=bsin B,
即a·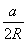 =b·
=b·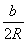 (其中R是△ABC外接圆的半径),所以a=b.所以△ABC为等腰三角形.
(其中R是△ABC外接圆的半径),所以a=b.所以△ABC为等腰三角形.
(2)由题意,可知m·p=0,即a(b-2)+b(a-2)=0,所以a+b=ab,由余弦定理,知4=c2=a2+b2-2abcos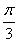 =(a+b)2-3ab,即(ab)2-3ab-4=0,所以ab=4或ab=-1(舍去).
=(a+b)2-3ab,即(ab)2-3ab-4=0,所以ab=4或ab=-1(舍去).
所以S△ABC=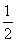 absin C=
absin C=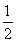 ×4×sin
×4×sin 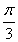 =
=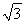 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目