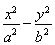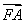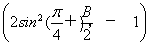题目内容
已知数列{an}成等比数列,且an>0.
(1)若a2-a1=8,a3=m.①当m=48时,求数列{an}的通项公式;②若数列{an}是唯一的,求m的值;
(2)若a2k+a2k-1+…+ak+1-(ak+ak-1+…+a1)=8,k∈N*,求a2k+1+a2k+2+…+a3k的最小值.
(1)见解析(2)32
【解析】设公比为q,则由题意,得q>0.
(1)①由a2-a1=8,a3=m=48,得
解之,得 或
或
所以数列{an}的通项公式为
an=8(2-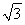 )(3+
)(3+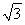 )n-1,或an=8(2+
)n-1,或an=8(2+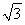 )(3-
)(3-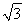 )n-1.
)n-1.
②要使满足条件的数列{an}是唯一的,即关于a1与q的方程组 有唯一正数解,即方程8q2-mq+m=0有唯一解.
有唯一正数解,即方程8q2-mq+m=0有唯一解.
由Δ=m2-32m=0,a3=m>0,所以m=32,此时q=2.
经检验,当m=32时,数列{an}唯一,其通项公式是an=2n+2.
(2)由a2k+a2k-1+…+ak+1-(ak+ak-1+…+a1)=8,
得a1(qk-1)(qk-1+qk-2+…+1)=8,且q>1.
a2k+1+a2k+2+…+a3k=a1q2k(qk-1+qk-2+…+1)=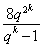 =8
=8
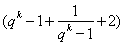 ≥32,
≥32,
当且仅当qk-1=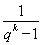 ,即q=
,即q=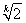 ,a1=8(
,a1=8(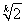 -1)时,
-1)时,
a2k+1+a2k+2+…+a3k的最小值为32

练习册系列答案
相关题目
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图,下列关于函数f(x)的四个命题:
x | -1 | 0 | 4 | 5 |
f(x) | 1 | 2 | 2 | 1 |

①函数y=f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.其中真命题的个数是________.