题目内容
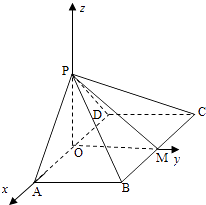
【题目】如图,四棱锥P﹣ABCD中,ABCD为矩形,平面PAD⊥平面ABCD. 
(1)求证:AB⊥PD;
(2)若∠BPC=90°,PB= ![]() ,PC=2,问AB为何值时,四棱锥P﹣ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P﹣ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
【答案】
(1)证明:∵在四棱锥P﹣ABCD中,ABCD为矩形,∴AB⊥AD,
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴AB⊥面PAD,∴AB⊥PD
(2)解:过P做PO⊥AD,∴PO⊥平面ABCD,
作OM⊥BC,连接PM
∴PM⊥BC,
∵∠BPC=90°,PB= ![]() ,PC=2,
,PC=2,
∴BC= ![]() ,PM=
,PM= ![]() =
= ![]() =
= ![]() ,BM=
,BM= ![]() =
= ![]() ,
,
设AB=x,∴OM=x∴PO= ![]() ,
,
∴VP﹣ABCD= ![]() ×x×
×x× ![]() ×
× ![]() =
= ![]()
![]() =
= ![]() ,
,
当 ![]() ,即x=
,即x= ![]() ,VP﹣ABCD=
,VP﹣ABCD= ![]() ,
,
建立空间直角坐标系O﹣AMP,如图所示,
则P(0,0, ![]() ),D(﹣
),D(﹣ ![]() ,0,0),C(﹣
,0,0),C(﹣ ![]() ,
, ![]() ,0),M(0,
,0),M(0, ![]() ,0),B(
,0),B( ![]() ,
, ![]() ,0)
,0)
面PBC的法向量为 ![]() =(0,1,1),面DPC的法向量为
=(0,1,1),面DPC的法向量为 ![]() =(1,0,﹣2)
=(1,0,﹣2)
∴cosθ= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() .由图可知二面角为锐角,即cos
.由图可知二面角为锐角,即cos ![]()
【解析】(1)要证AD⊥PD,可以证明AB⊥面PAD,再利用面面垂直以及线面垂直的性质,即可证明AB⊥PD.(2)过P做PO⊥AD得到PO⊥平面ABCD,作OM⊥BC,连接PM,由边长关系得到BC= ![]() ,PM=
,PM= ![]() ,设AB=x,则VP﹣ABCD=
,设AB=x,则VP﹣ABCD= ![]()
![]() ,故当
,故当 ![]() 时,VP﹣ABCD取最大值,建立空间直角坐标系O﹣AMP,利用向量方法即可得到夹角的余弦值.
时,VP﹣ABCD取最大值,建立空间直角坐标系O﹣AMP,利用向量方法即可得到夹角的余弦值.

【题目】某校高三年级共有学生![]() 名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为
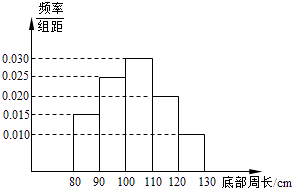
名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为![]() 分)进行统计,绘制出如下尚未完成的频率分布表:
分)进行统计,绘制出如下尚未完成的频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
(1)补充完整题中的频率分布表;
(2)若成绩在![]() 为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
【题目】教材上一例问题如下:
一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表,试建立y与x之间的回归方程.
温度 x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
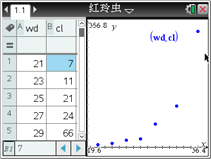
某同学利用图形计算器研究它时,先作出散点图(如图所示),发现两个变量不呈线性相关关系. 根据已有的函数知识,发现样本点分布在某一条指数型曲线![]() 的附近(
的附近(![]() 和
和![]() 是待定的参数),于是进行了如下的计算:
是待定的参数),于是进行了如下的计算:
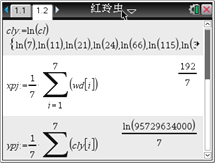
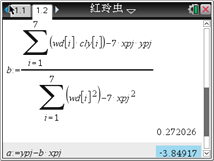
根据以上计算结果,可以得到红铃虫的产卵数y对温度x的回归方程为__________.(精确到0.0001) (提示:![]() 利用代换可转化为线性关系)
利用代换可转化为线性关系)