题目内容
(12分)已知函数
(Ⅰ)当 时,求函数
时,求函数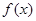 的最小值;
的最小值;
(Ⅱ)若对任意 ,
, 恒成立,试求实数
恒成立,试求实数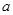 的取值范围.
的取值范围.
(Ⅰ) 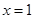 时,
时,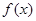 取得最小值
取得最小值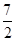 .(Ⅱ)
.(Ⅱ) 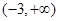 .
.
解析试题分析:(1)先将原式化成求解导数f‘(x),再利用导数的正负与函数单调性的关系,即可求得函数f(x)的最小值;
(2)原题等价于x2+2x+a>0对x∈[1,+∞)恒成立,再结合二次函数的单调性只须g(1)>0,从而求得实数a的取值范围;
解(Ⅰ)  时,
时,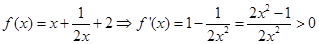 (因为
(因为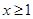 )
)
所以,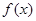 在
在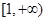 上单调递增,故
上单调递增,故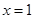 时,
时,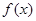 取得最小值
取得最小值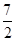 .
.
(Ⅱ) 因为对任意 ,
, 恒成立,即
恒成立,即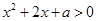 恒成立,只需
恒成立,只需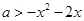 恒成立,只需
恒成立,只需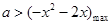 ,因为
,因为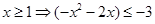 ,
,
所以,实数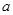 的取值范围是
的取值范围是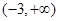 .
.
考点:本题主要考查了函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
点评:解决该试题的关键是是对于同一个问题的不同的处理角度,可以运用均值不等式得到最值,也可以结合导数的工具得到最值,对于恒成立问题一般都是转换为求解函数的 最值即可得到。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 定义域为
定义域为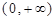 ,且
,且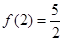 .
.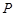 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点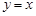 和
和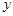 轴的垂线,垂足分别为
轴的垂线,垂足分别为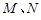 .
.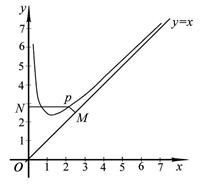
 的单调递减区间(不必证明);(4分)
的单调递减区间(不必证明);(4分)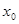 ,求
,求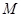 点的坐标(用
点的坐标(用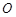 为坐标原点,求四边形
为坐标原点,求四边形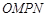 面积的最小值.(7分)
面积的最小值.(7分)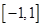 上的偶函数
上的偶函数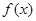 ,已知当
,已知当 时的解析式
时的解析式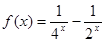
 在
在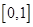 上的解析式;
上的解析式;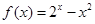 ,问方程
,问方程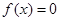 在区间[-1,0]内是否有
在区间[-1,0]内是否有 在(0,1)内恰有一解,求实数
在(0,1)内恰有一解,求实数 的取值范围.
的取值范围.  =
=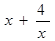
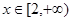 上是增函数;(2)求
上是增函数;(2)求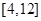 上的值域。
上的值域。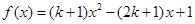 ,
, .
.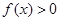 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 时,
时, 恒成立,求实数
恒成立,求实数 时,解不等式
时,解不等式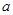 为非负实数,函数
为非负实数,函数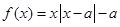 .
.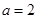 时,求函数的单调区间;
时,求函数的单调区间;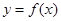 的零点个数.
的零点个数. (
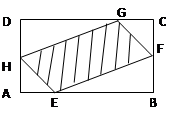
(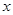 ,绿地面积为
,绿地面积为 .
.

 的最小值;
的最小值;  的值域。
的值域。