题目内容
(本题满分14分)设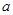 为非负实数,函数
为非负实数,函数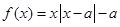 .
.
(Ⅰ)当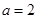 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)讨论函数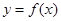 的零点个数.
的零点个数.
(Ⅰ) 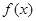 的单调递增区间是
的单调递增区间是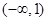 和
和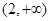 ,单调递减区间是
,单调递减区间是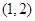 .
.
(Ⅱ)当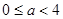 时,函数有一个零点;
时,函数有一个零点;
当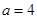 时,函数有两个零点;
时,函数有两个零点;
当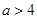 时,函数有三个零点.
时,函数有三个零点.
解析试题分析:(Ⅰ)当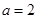 时,
时,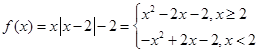 ,然后对于分段函数各段的情况分别说明单调性,整体来合并得到结论。
,然后对于分段函数各段的情况分别说明单调性,整体来合并得到结论。
(2)当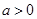 时,
时,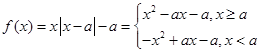 ,
,
故当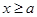 时,
时,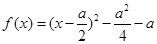 ,二次函数对称轴
,二次函数对称轴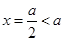 ,那么结合二次函数的 性质可知顶点的函数值为正数,负数,还是零,来确定零点的问题。
,那么结合二次函数的 性质可知顶点的函数值为正数,负数,还是零,来确定零点的问题。
解:(Ⅰ)当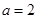 时,
时,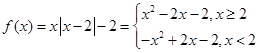 ,
,
① 当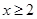 时,
时, ,∴
,∴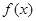 在
在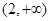 上单调递增;
上单调递增;
② 当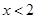 时,
时, ,
,
∴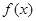 在
在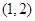 上单调递减,在
上单调递减,在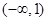 上单调递增;
上单调递增;
综上所述,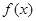 的单调递增区间是
的单调递增区间是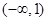 和
和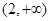 ,单调递减区间是
,单调递减区间是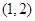 .
.
(Ⅱ)(1)当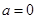 时,
时,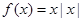 ,函数
,函数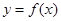 的零点为
的零点为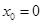 ;
;
(2)当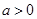 时,
时,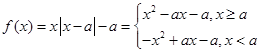 ,
,
故当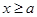 时,
时,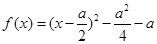 ,二次函数对称轴
,二次函数对称轴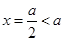 ,
,
∴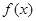 在
在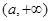 上单调递增,又
上单调递增,又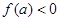 ,f(x)与x轴在
,f(x)与x轴在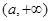 有唯一交点;
有唯一交点;
当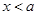 时,
时,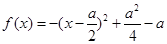 ,二次函数对称轴
,二次函数对称轴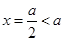 ,
,
∴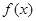 在
在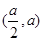 上单调递减,在
上单调递减,在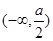 上单调递增;∴
上单调递增;∴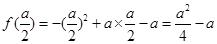 ,
, 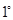 当
当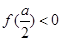 ,即
,即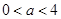 时,函数
时,函数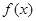 与
与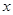 轴只有唯一交点,即唯一零点,
轴只有唯一交点,即唯一零点,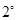 当
当 ,即
,即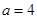 时,函数
时,函数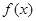 与
与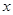 轴有两个交点,即两个零点
轴有两个交点,即两个零点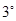 当
当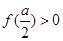 ,即
,即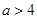 时,f(a)<0,函数
时,f(a)<0,函数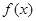 与
与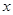 轴有三个交点,即有三个零点
轴有三个交点,即有三个零点
综上可得,当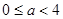 时,函数有一个零点;
时,函数有一个零点;
当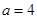 时,函数有两个零点;
时,函数有两个零点;
当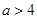 时,函数有三个零点.
时,函数有三个零点.
考点:本题主要考查了函数单调性和函数的零点的运用。
点评:解决该试题的关键是对于参数的分类讨论是否能够很好的全面的表示出不同情况下的零点,也是该试题一个难点。

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
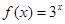 ,且
,且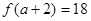 ,
,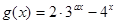 。
。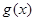 的解析式; (2)求函数
的解析式; (2)求函数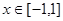 上的值域。
上的值域。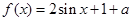 是一个奇函数.
是一个奇函数.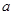 的值和
的值和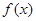 的值域;
的值域; >
> ,若
,若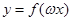 在区间
在区间 是增函数,求
是增函数,求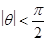 ,若对
,若对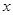 取一切实数,不等式
取一切实数,不等式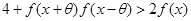 都成立,求
都成立,求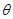 的取值范围.
的取值范围.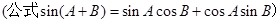

 时,求函数
时,求函数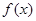 的最小值;
的最小值; ,
, 恒成立,试求实数
恒成立,试求实数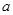 的取值范围.
的取值范围.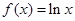 ,
, ,设
,设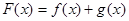 .
.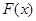 的单调区间;
的单调区间;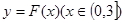 图象上任意一点
图象上任意一点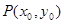 为切点的切线的斜率
为切点的切线的斜率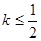
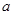 的最小值.
的最小值. ,使得函数
,使得函数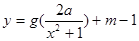 的图象与
的图象与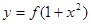 的图
的图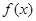 在定义域上是奇函数,且在
在定义域上是奇函数,且在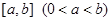 上是减函数,图像如图所示.
上是减函数,图像如图所示.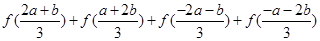 ;
; 上的图像;
上的图像;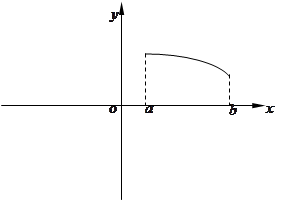
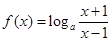 (
(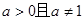 ).
).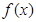 的奇偶性,并证明;
的奇偶性,并证明;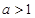 ,用单调性定义证明函数
,用单调性定义证明函数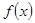 在区间
在区间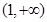 上单调递减;
上单调递减; ,使得
,使得 时,值域为
时,值域为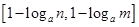 ,若存在,求出实数
,若存在,求出实数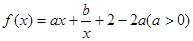 的图像在点
的图像在点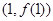 处的切线与直线
处的切线与直线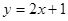 平行.
平行.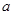 ,
,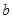 满足的关系式;
满足的关系式;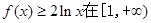 上恒成立,求
上恒成立,求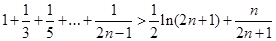 (
( )
)